Fingsinz's space | 风信梓

OpenCV图像处理基础学习记录

一、Visual Studio2022配置OpencCV
二、基本操作
三、灰度变换
四、直方图处理
五、空间滤波基础
六、频率域滤波
七、噪声模型及估计和滤波方法
八、滤波器
九、彩色图像处理基础
十、图像形态学处理
十一、图像分割
1. 11.1 图像边缘检测
2. 11.2 图像阈值分割

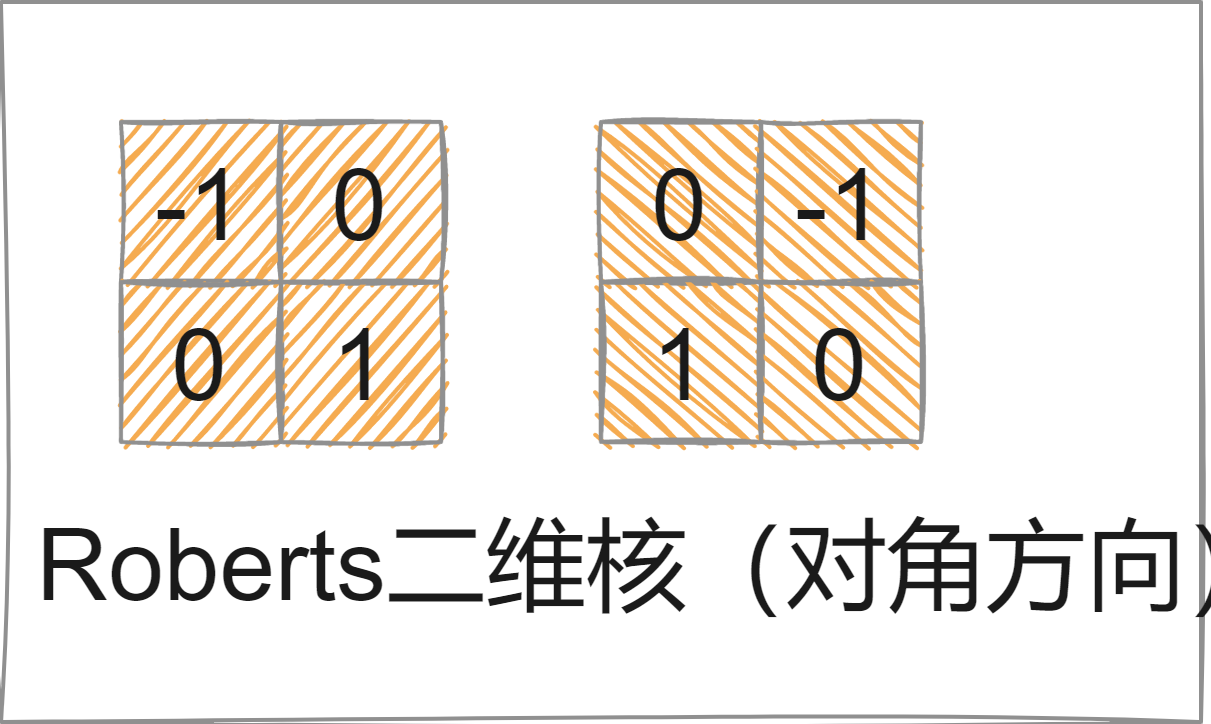
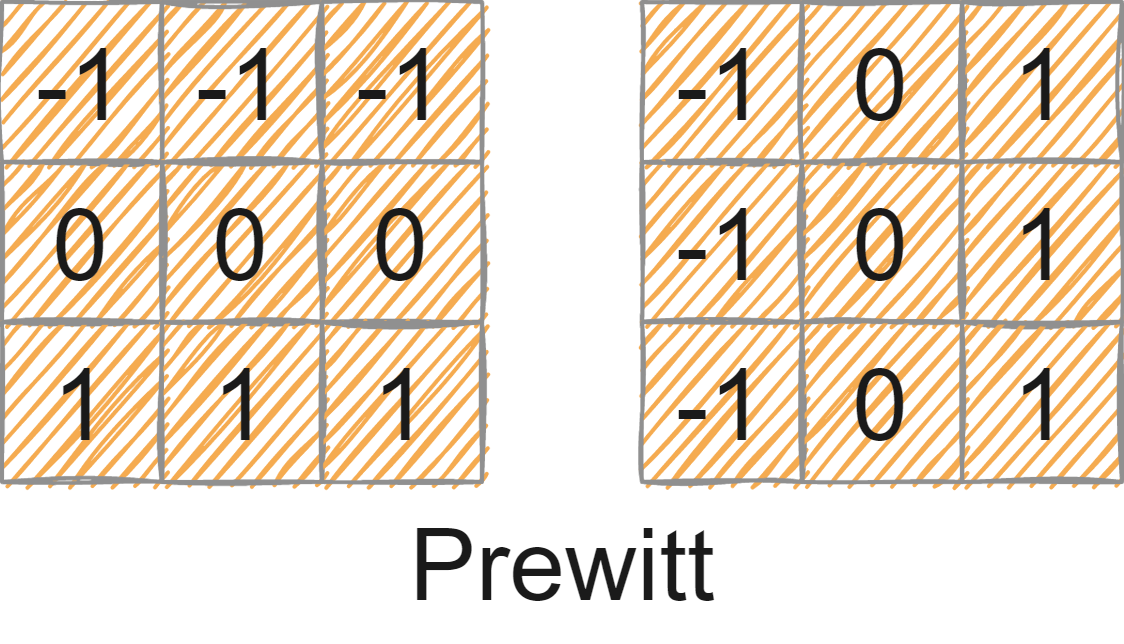
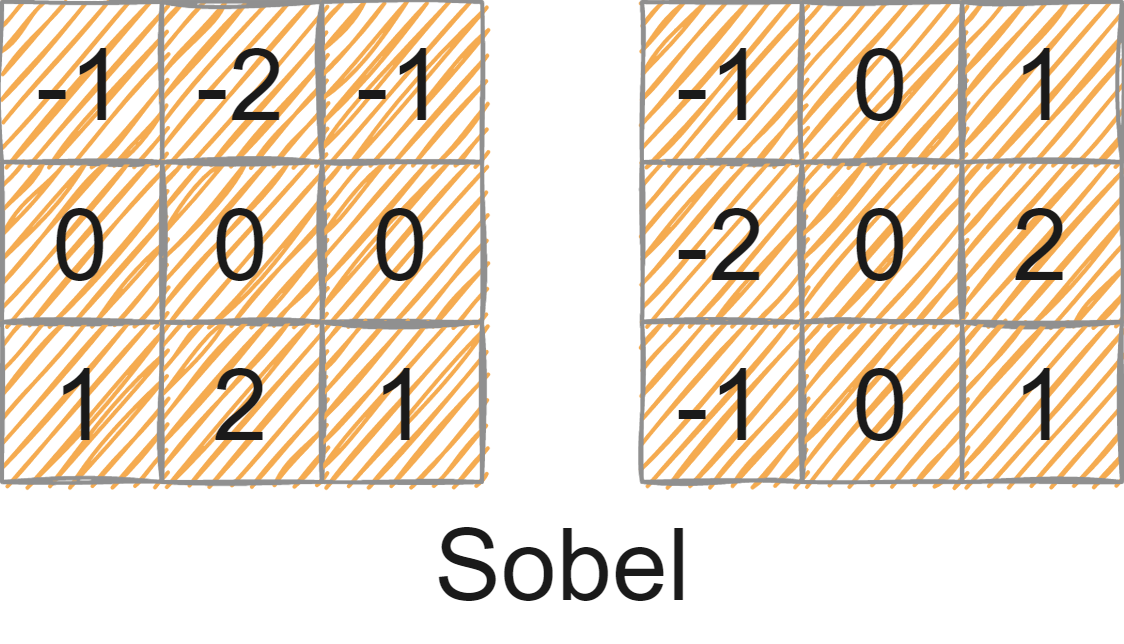
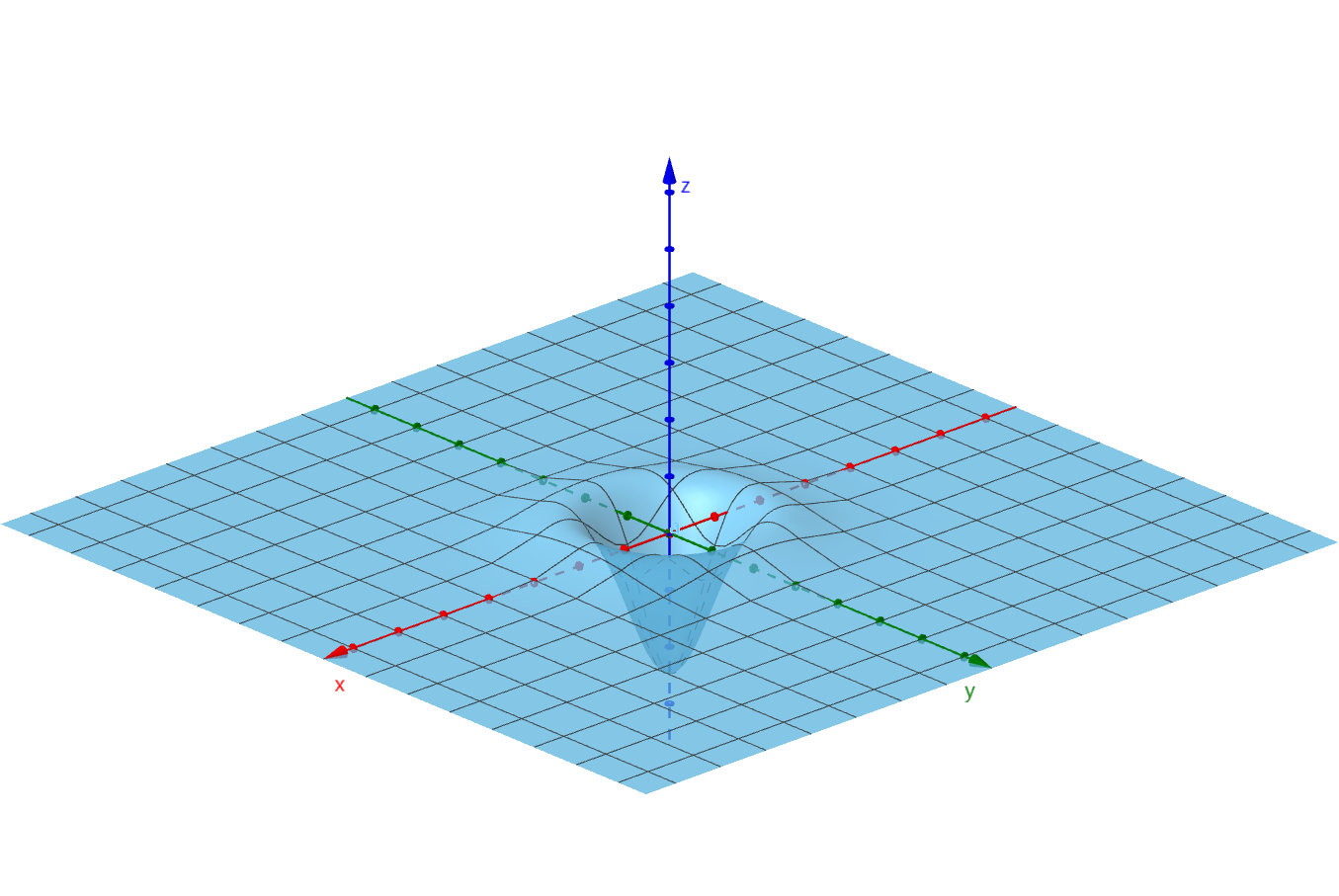
关键词：C++、OpenCV、图像处理

一、Visual Studio2022配置OpencCV

1.1 下载OpenCV并安装

可以直接前往OpenCV官网进行下载资源。

有两种形式可以下载安装：

Windows的exe可执行文件安装。

exe文件安装后有OpenCV静态库和动态库文件，可以直接链接到VS使用，整体更方便。

Sources源码安装。

下载源码后需要自己编译生成OpenCV的静态库和动态库。

1.2 VS中配置OpenCV

我下载的OpenCV版本为4.5.2，目录在： D:\opencv4.5.2

在VS中新建项目，右键项目点击属性，做以下操作：

VC++ 目录 → 包含目录添加OpenCV的include目录。例如，我的操作是把 D:\opencv4.5.2\build\include 添加到包含目录。
VC++ 目录 → 库目录添加OpenCV的x64/vc15/lib目录。例如，我的操作是把 D:\opencv4.5.2\build\x64\vc15\lib 添加到库目录。
链接器 → 输入 → 附加依赖项添加OpenCV的动态库。例如，我的操作是：debug版本添加 opencv_world452d.lib，release版本添加 opencv_world452.lib。

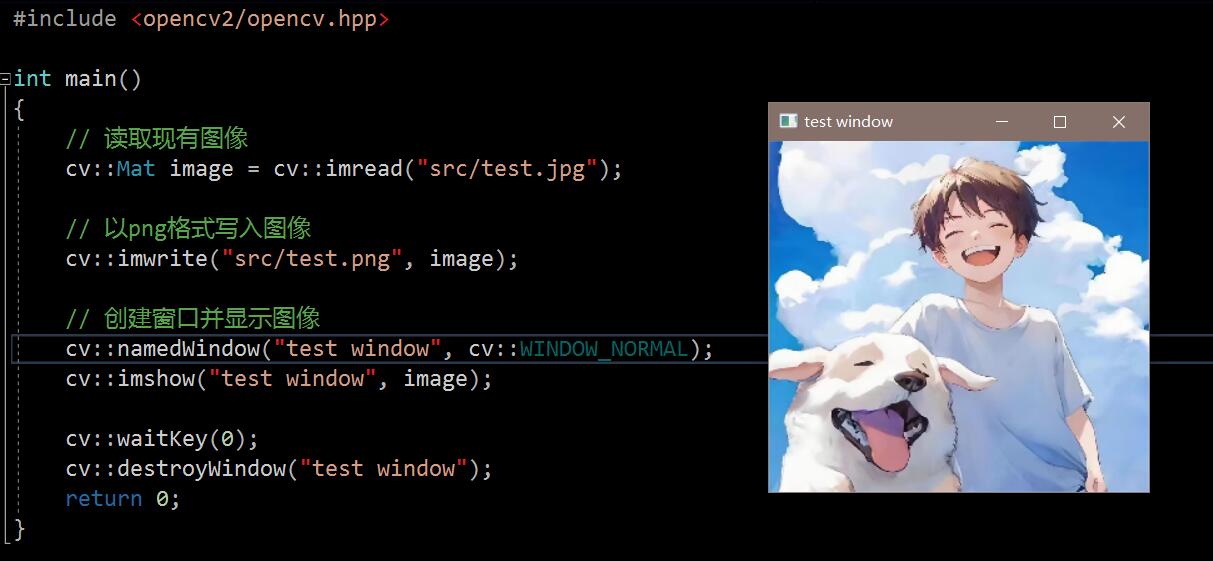
1.3 测试OpenCV

新建Cpp文件，复制以下代码：

#include <opencv2/opencv.hpp>

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::imshow("a", image);
    cv::waitKey(0);
    return 0;
}

编译链接测试，若能运行，则说明配置正确。

二、基本操作

2.1 读写图像

2.1.1 相关函数

读取图像

函数原型：

1	Mat imread(const String& filename, int flags = IMREAD_COLOR)

第一参数为图像路径，第二参数为加载图像的形式（默认加载彩色图像）。

第二参数可选参数有三种：

0 或 IMREAD_GRAYSCALE ，表示加载灰度图像。
1 或 IMREAD_COLOR ，表示加载彩色图像（默认）。
-1 或 IMREAD_UNCHANGED ，表示加载包括alpha通道。

创建窗口

函数原型：

1	void namedWindow(const String& winname, int flags = WINDOW_AUTOSIZE)

第一参数为窗口名字，第二参数为窗口形式。

窗口形式常用有两种：

WINDOW_AUTOSIZE 表示固定大小（默认）。
WINDOW_NORMAL 表示可调节大小。

显示图像

函数原型：

1	void imshow(const String& winname, InputArray mat)

第一参数为窗口名字，第二参数为图像对象名称。

写入图像

函数原型：

1	bool imwrite( const String& filename, InputArray img, const std::vector<int>& params = std::vector<int>())

第一参数为存储图像路径，第二参数为图像对象名称，其余参数不重要。

等待延时

函数原型：

1	int waitKey(int delay = 0)

参数为延时的毫秒数，默认为0，即无限时等待键盘输入。

窗口销毁

函数原型：

1	void destroyWindow(const String& winname)

参数为销毁的窗口名称，一般情况下系统会自动回收。

2.1.2 示例代码

#include <opencv2/opencv.hpp>

int main()
{
    // 读取现有图像
    cv::Mat image = cv::imread("src/test.jpg");

    // 以png格式写入图像
    cv::imwrite("src/test.png", image);

    // 创建窗口并显示图像
    cv::namedWindow("test window", cv::WINDOW_NORMAL);
    cv::imshow("test window", image);

    cv::waitKey(0);
    cv::destroyWindow("test window");
    return 0;
}

2.2 读写视频

2.2.1 相关概念

VideoCapture类

VideoCapture类提供了有关视频的操作：

1	cv::VideoCapture cap(0);

创建VideoCapture实例，使用构造函数，传入参数0表示设备0。

1	bool isOpened()

确认摄像头是否开启成功。

1	bool grab()

确认摄像头在运行中是否捕获到帧。

1	bool read(OutputArray image)

将视频捕获对象中捕获到的图像输出到image中。

转化图像颜色通道

函数原型：

1	void cvtColor(InputArray src, OutputArray dst, int code, int dstCn = 0)

第一参数是输入图像，第二参数是输出图像，第三参数是转化图像颜色通道代码，第四参数暂不管。

转化图像颜色通道代码有许多，通常用到：

COLOR_BGR2GRAY ：由OpenCV的BGR通道转为灰度通道。
COLOR_BGR2BGRA ：由OpenCV的BGR通道添加了Alpha通道。

读取、显示视频

与使用摄像头的思路类似，将捕获设备改为捕获本地文件。

1	cv::VideoCapture cap("src/test.mp4");

显示与使用摄像头的思路类似，捕获视频每一帧并展示图像对象。

写入视频

定义编解码器并创建VideoWriter对象进行保存。

1 2	int fourcc = cv::VideoWriter::fourcc('X', 'V', 'I', 'D'); // 编解码器 cv::VideoWriter out("output.avi", fourcc, 20.0, cv::Size(640, 480));

VideoWriter的其中一个构造函数原型如下：

1	VideoWriter(const String& filename, int fourcc, double fps, Size frameSize, bool isColor = true)

2.2.2 示例代码

#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::VideoCapture cap(0);
    cv::Mat img;
    int fourcc = cv::VideoWriter::fourcc('X', 'V', 'I', 'D');
    cv::VideoWriter out("output.avi", fourcc, 20.0, cv::Size(640, 480));

    while (cap.isOpened())
    {
        if (!cap.grab())
        {
            std::cout << "摄像头错误" << std::endl;
            break;
        }
        out.write(img);
        cap.read(img);
        cv::imshow("video", img);
        if (cv::waitKey(1) == 'q')    break;
    }

    cap.release();  // 释放视频捕获对象
    out.release();  // 释放视频写入对象
    cv::destroyWindow("video");
    return 0;
}

2.3 图像的基本操作

2.3.1 创建空白图像

使用 Mat 创建图像矩阵的常用形式：

创建空图像，大小为0：

1	cv::Mat image1;

指定矩阵大小，指定数据类型

1	cv::Mat image2(100, 100, CV_8U);

创建100行×100列的矩阵，数据类型为无符号8位int，即灰度图像。
还有一种常用的类型CV_8UC3，表示三通道无符号8位int。

指定矩阵大小，指定数据类型，设置初始值

1	cv::Mat image3(100, 100, CV_8U, 100)

创建100行×100列的矩阵，数据类型为无符号8位int灰度图像，灰度值为100。
对于三通道图像，应使用Scalar()：

1	cv::Mat image(640, 640, CV_8UC3, cv::Scalar(100, 100, 0));

2.3.2 获取图像信息

获取行列数、通道数

直接访问Mat类成员rows、cols和函数channels()返回图像的行、列和通道数。可以通过通道数判断是灰度图像（通道为1）还是彩色图像（通道为3）。

1
2
3

std::cout << "图像的行：" << image.rows << std::endl;
std::cout << "图像的列：" << image.cols << std::endl;
std::cout << "通道数：" << image.channels() << std::endl;

访问像素点的BGR值

通过Vec3b数据类型访问返回像素点的BGR值，注意，前者是行数，后者是列数。

int blue = image.at<cv::Vec3b>(100, 100)[0];
// 索引值0表示索引BGR值中的B，也就是蓝色通道的数值
int green = image.at<cv::Vec3b>(100, 100)[1];
int red = image.at<cv::Vec3b>(100, 100)[2];

同理进行修改：

1 2	image.at<cv::Vec3b>(100, 100)[0] = 201; // 将坐标(100, 100)的像素点蓝色数值改为201

当然大面积的修改才会明显，通过循环进行：

1
2
3

for(int i = 0; i < 100; ++ i)
    for (int j = 0; j < 100; ++ j)
        image.at<cv::Vec3b>(i, j)[0] = 100;

如果修改BGR值，则组成Vec3b类型：

1
2
3

for(int i = 0; i < 100; ++ i)
    for (int j = 0; j < 100; ++ j)
        image.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 0, 0);

2.3.3 标记区域

创建tmp变量，获取图像行从200到1000，列从200到1000的区域。将图像行从1200到2000，列从1200到2000的区域变成tmp

1
2
3

cv::Mat image = cv::imread("src/test.jpg");
cv::Mat tmp = image(cv::Range(100, 200), cv::Range(100, 200));
tmp.copyTo(image(cv::Range(200, 300), cv::Range(200, 300)));

2.3.4 遍历图像

循环行和列遍历图像

对于OpenCV的Mat，其顺序是行和列。与C++的二维数组类似，遍历：

1
2
3

for(int i = 0; i < 100; ++ i)
    for (int j = 0; j < 100; ++ j)
        image.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 0, 0);

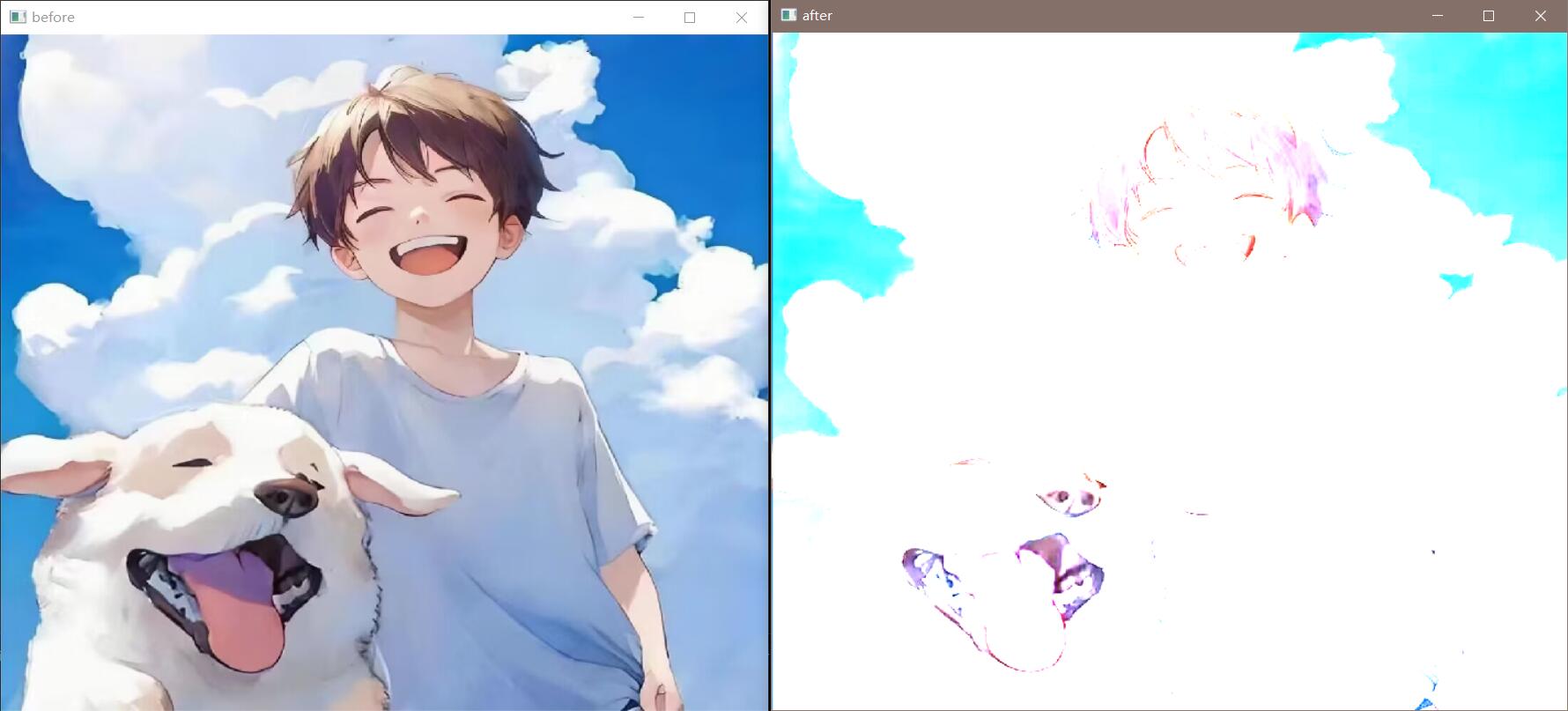
指针扫描

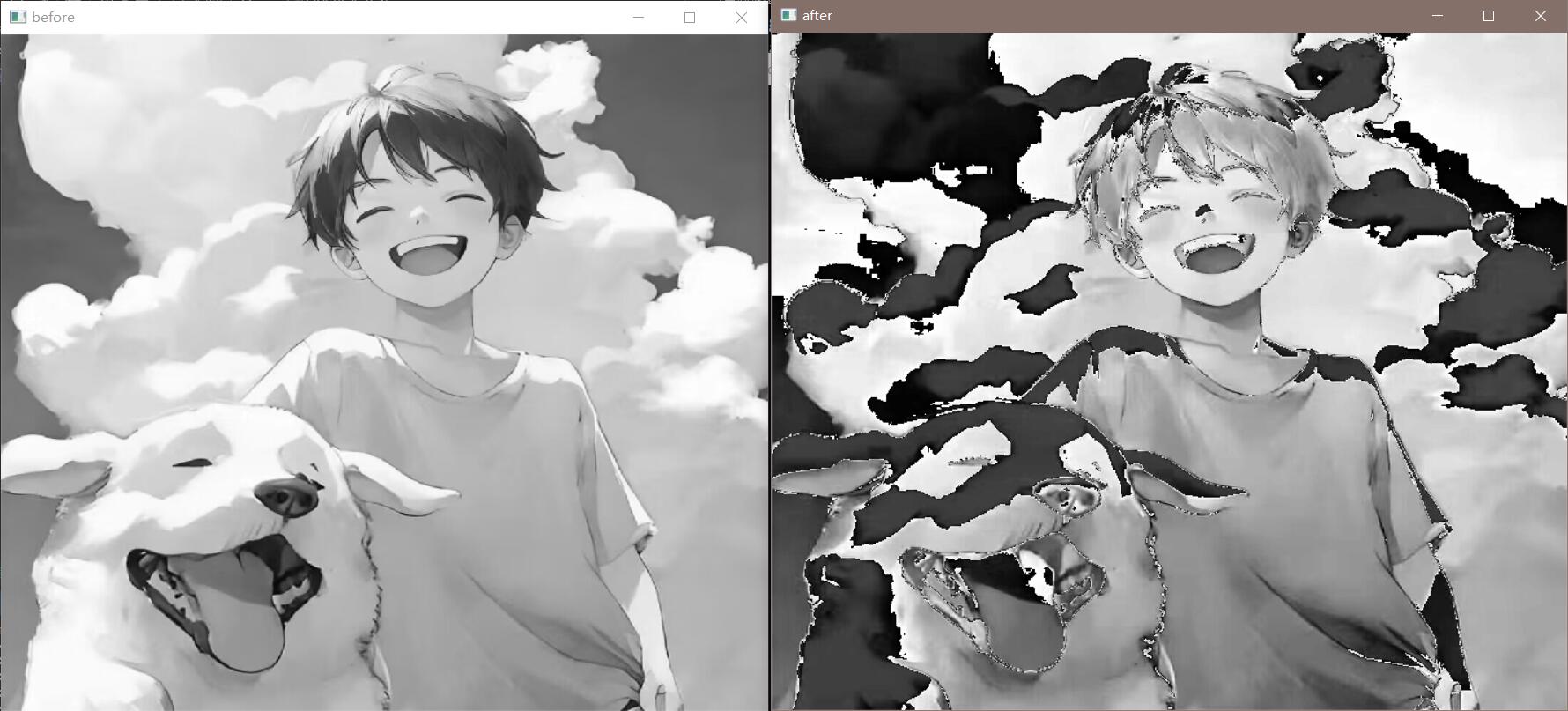
#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat img = cv::imread("src/test.jpg");
    cv::Mat output_img;
    output_img = cv::Mat(img.size(), img.type());   // 复制画布
    output_img = img.clone();    // 克隆像素值
    int r = img.rows, c = img.cols, channels = img.channels();


    for (int j = 0; j < r; j ++)
    {
        const uchar *now = img.ptr<uchar>(j);   // 原图当前行指针
        uchar *output = output_img.ptr<uchar>(j);   // 输出图像当前行指针
        // 实际上每一列都由通道数三个数据组成，所以实际上列数应该是通道数×列
        for (int i = channels; i < c * channels; i ++)
        {
            output[i] = cv::saturate_cast<uchar>(5 * now[i]);
            // saturate_cast保证了计算结果仍在0~255之间
        }
    }

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("before", img);
    cv::imshow("after", output_img);
    cv::waitKey(0);
    cv::destroyAllWindows();
    return 0;
}

2.4 绘图入门

2.4.1 静态绘制

绘制线

函数原型：

1	void line(InputOutputArray img, Point pt1, Point pt2, const Scalar& color,int thickness = 1, int lineType = LINE_8, int shift = 0)

参数分别为：图像对象、始点坐标、终点坐标、颜色、线粗细、线类型……

使用示例：

1	cv::line(image, cv::Point(0, 0), cv::Point(512, 512), cv::Scalar(255, 0, 0), 5);

绘制矩形

函数原型：

1	void rectangle(InputOutputArray img, Rect rec, const Scalar& color, int thickness = 1, int lineType = LINE_8, int shift = 0)

参数分别为：图像对象、矩形框、颜色、边框线粗细、边框线类型……

矩形框的四个参数分别为：x坐标、y坐标、宽、高。

使用示例：

1	cv::rectangle(image, cv::Rect(0, 0, 100, 100), cv::Scalar(0, 255, 255), 5);

绘制圆

函数原型：

1	void circle(InputOutputArray img, Point center, int radius, const Scalar& color, int thickness = 1, int lineType = LINE_8, int shift = 0)

参数分别为：图像对象、圆心、半径、颜色、边框线粗细、边框线类型……

使用示例：

1	cv::circle(image, cv::Point(319, 319), 50, cv::Scalar(0, 0, 255), 5);

绘制椭圆

函数原型：

1	void ellipse(InputOutputArray img, Point center, Size axes, double angle, double startAngle, double endAngle, const Scalar& color, int thickness = 1, int lineType = LINE_8, int shift = 0)

参数分别为：图像对象、中心点、长短轴、初始旋转角度、椭圆开始角度、椭圆结束角度、颜色、边框线粗细、边框线类型……边框线粗细为-1表示内填充。

使用示例：

1	cv::ellipse(image, cv::Point(319, 119), cv::Size(100, 50), 0, 180, 360, 255, -1);

绘制多边形

函数原型：

1	void polylines(InputOutputArray img, const Point* const* pts, const int* npts, int ncontours, bool isClosed, const Scalar& color, int thickness = 1, int lineType = LINE_8, int shift = 0 )

参数分别为：图像对象、const修饰的指向多边形数组的指针、多边形顶点个数的数组名、绘制多边形的个数、是否闭合、颜色、边框粗细、边框线类型

使用示例：

// 构造多边形的端点形成的点类型数组。
cv::Point pts[] = { cv::Point(10, 5), cv::Point(20, 30), cv::Point(70, 20), cv::Point(50, 10) };

// const修饰的多边形数组指针
const cv::Point *ppt[1] = { pts };

// 多边形顶点个数的数组名
int npt[] = { 4 };
cv::polylines(image, ppt, npt, 1, true, cv::Scalar(0, 255, 255));

添加文本

函数原型：

1	void putText( InputOutputArray img, const String& text, Point org, int fontFace, double fontScale, Scalar color, int thickness = 1, int lineType = LINE_8, bool bottomLeftOrigin = false )

参数分别为：图像对象、文本内容、文字在图像中的左下角坐标、字体、字体大小、字体颜色、字体粗细、描绘字体的线类型……

使用示例：

1	cv::putText(image, "OpenCV", cv::Point(10, 500), cv::FONT_HERSHEY_SIMPLEX, 4, cv::Scalar(255, 255, 255), 2, cv::LINE_AA);

整体绘制展示

#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat image(640, 640, CV_8UC3);

    cv::line(image, cv::Point(0, 0), cv::Point(512, 512), cv::Scalar(255, 0, 0), 5);
    cv::rectangle(image, cv::Rect(0, 0, 100, 100), cv::Scalar(0, 255, 255), 5);
    cv::circle(image, cv::Point(319, 319), 50, cv::Scalar(0, 0, 255), 5);
    cv::ellipse(image, cv::Point(319, 119), cv::Size(100, 50), 0, 180, 360, 255, -1);

    cv::Point pts[] = { cv::Point(10, 5), cv::Point(20, 30), cv::Point(70, 20), cv::Point(50, 10) };
    const cv::Point *ppt[1] = { pts };
    int npt[] = { 4 };
    cv::polylines(image, ppt, npt, 1, true, cv::Scalar(0, 255, 255));
    cv::putText(image, "OpenCV", cv::Point(10, 500), cv::FONT_HERSHEY_SIMPLEX, 4, cv::Scalar(255, 255, 255), 2, cv::LINE_AA);

    cv::namedWindow("img", cv::WINDOW_NORMAL);
    cv::imshow("img", image);
    cv::waitKey(0);
    return 0;
}

2.4.2 鼠标绘制

#include <opencv2/opencv.hpp>
#include <iostream>

cv::Mat image(640, 640, CV_8UC3);    // 画布
bool drawing = false;    // 是否绘画
bool mode = true;        // 矩形绘制还是圆形绘制
int ix, iy = -1;
int r, g, b, t = 0;


// 绘画函数
void draw(int event, int x, int y, int flags, void *param)
{
    if (event == cv::EVENT_LBUTTONDOWN)    // 当鼠标按下时
    {
        drawing = true;        // 启动绘画
        ix = x;                // 获取起点坐标
        iy = y;
    }
    else if (event == cv::EVENT_MOUSEMOVE)    // 当鼠标移动时
    {
        if (drawing)    // 处于绘画状态
        {
            if (mode)    // 矩形绘制时
            {
                cv::rectangle(image, cv::Point(ix, iy), cv::Point(x, y), cv::Scalar(b, g, r), t * 20);
            }
            else        // 圆形绘制时
            {
                cv::circle(image, cv::Point(x, y), 5, cv::Scalar(b, g, r), t * 20);
            }
        }
    }
    else if (event == cv::EVENT_LBUTTONUP)    // 当鼠标松开时
    {
        drawing = false;    // 关闭绘画
        if (mode)    // 补上最后一笔， x和y是当前的坐标
        {
            cv::rectangle(image, cv::Point(ix, iy), cv::Point(x, y), cv::Scalar(b, g, r), t * 20);
        }
        else
        {
            cv::circle(image, cv::Point(x, y), 5, cv::Scalar(b, g, r), t * 20);
        }
    }
}

int main()
{
    cv::namedWindow("image", cv::WINDOW_NORMAL);
    cv::setMouseCallback("image", draw);    // 绑定画布和回调函数
    cv::createTrackbar("R", "image", 0, 255);    // 轨迹栏
    cv::createTrackbar("G", "image", 0, 255);
    cv::createTrackbar("B", "image", 0, 255);
    cv::createTrackbar("Thickness", "image", 0, 5);

    while (true)
    {
        cv::imshow("image", image);
        int k = cv::waitKey(1) & 0xFF;
        if (k == 'q')
        {
            break;
        }
        else if (k == 'm')
        {
            mode = !mode;
        }
        r = cv::getTrackbarPos("R", "image");    // 刷新绘图属性
        g = cv::getTrackbarPos("G", "image");
        b = cv::getTrackbarPos("B", "image");
        t = cv::getTrackbarPos("Thickness", "image");
    }
    cv::destroyAllWindows();
    return 0;
}

三、灰度变换

3.1 灰度变换原理

通过变换函数T将原图像像素灰度值r映射为灰度值s：

s=T(r)

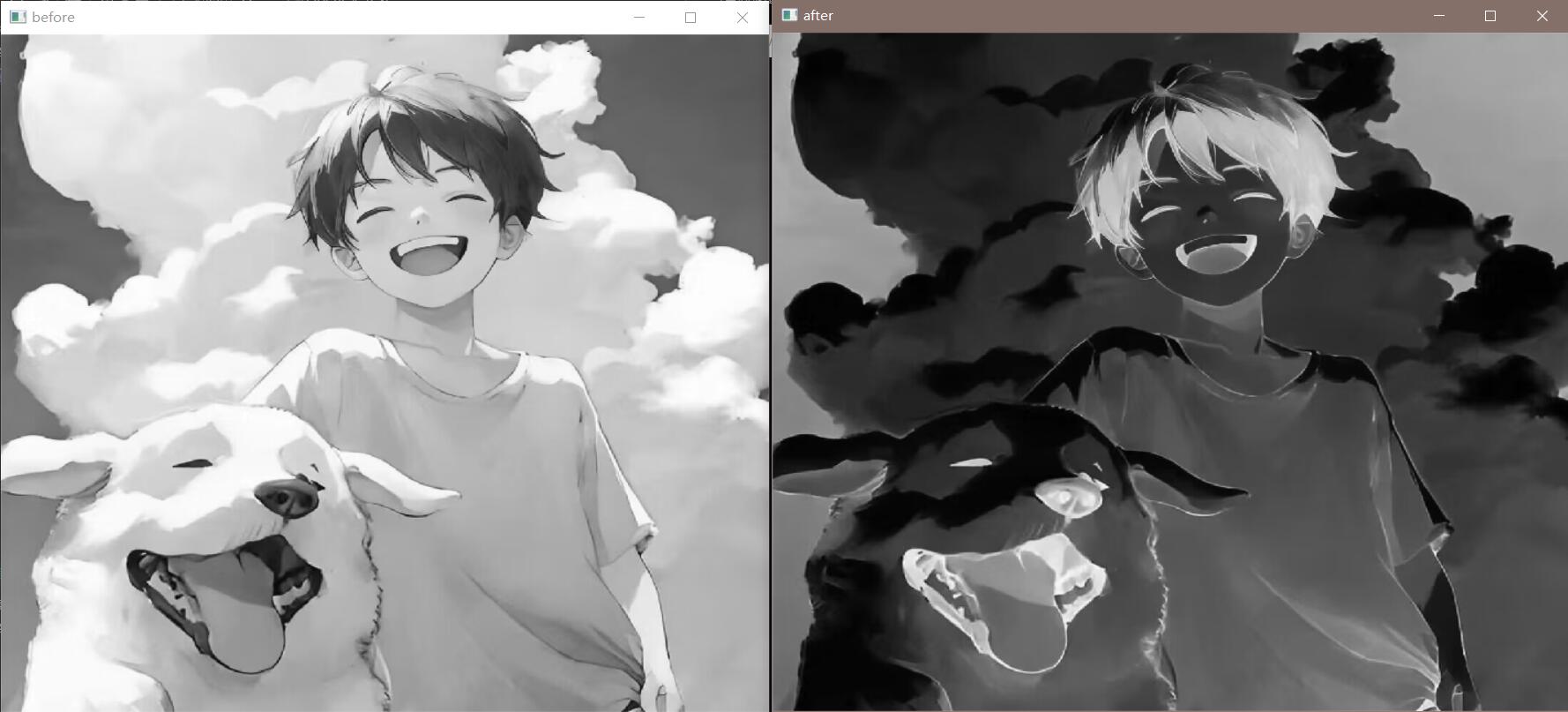
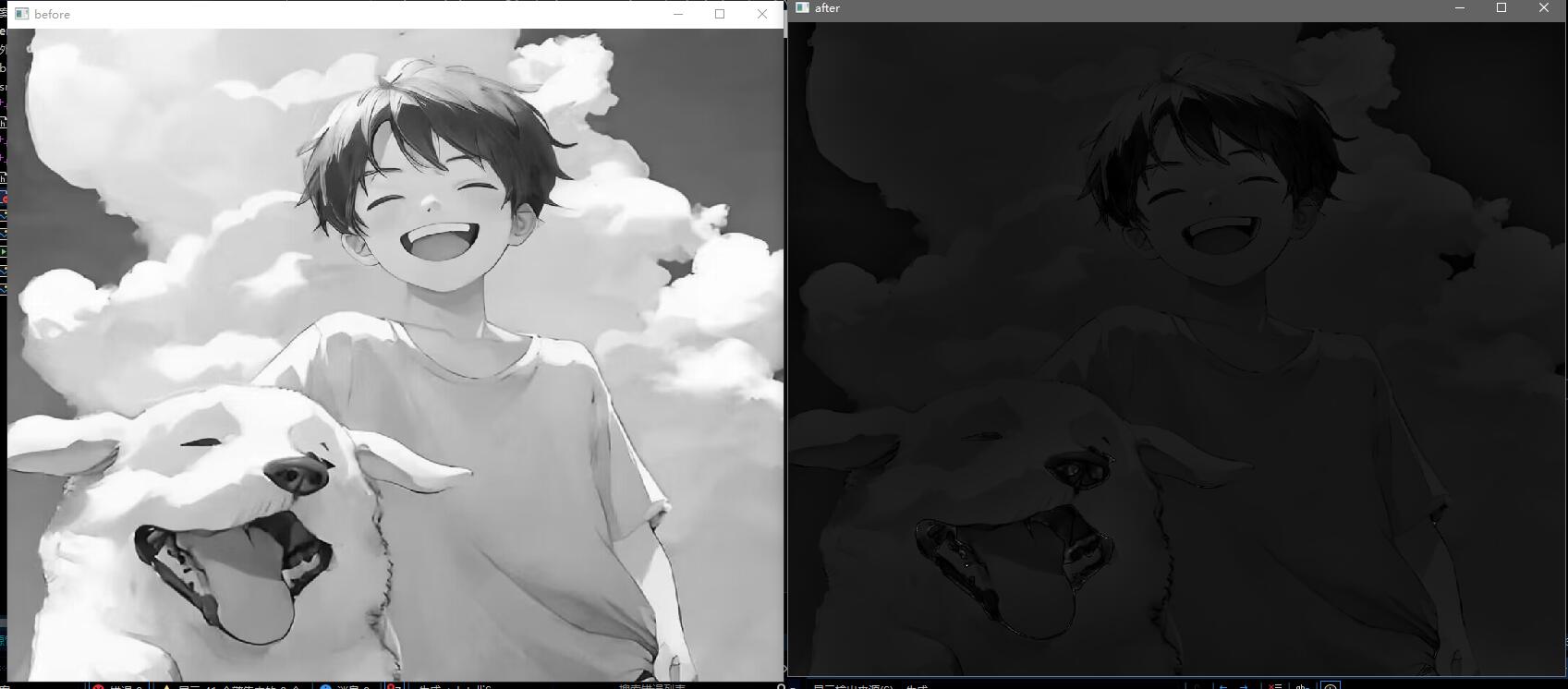
3.2 灰度反转

灰度反转：将图像亮暗对调，可以增强图像中的暗色区域细节。

s = T(r) = L - 1 - r，其中L为图像灰度级，0~255灰度图像的灰度级为256

进行 $s = T(r) = 256 - 1 - r$ 代码：

#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat output_image, image_gray;
    cv::cvtColor(image, image_gray, cv::COLOR_BGR2GRAY);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image_gray);

    output_image = image_gray.clone();

    for (int i = 0; i < image_gray.rows; ++ i)
        for (int j = 0; j < image_gray.cols; ++ j)
            output_image.at<uchar>(i, j) = 255 - image_gray.at<uchar>(i, j);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", output_image);

    cv::waitKey(0);

    return 0;
}

效果展示：

3.3 对数变换

对数变换：扩展图像中的暗像素值，压缩高灰度值。

s = T(r) = c\log(1 + r)

其中有一个图像归一化的过程，使用函数：

1	void normalize( InputArray src, InputOutputArray dst, double alpha = 1, double beta = 0, int norm_type = NORM_L2, int dtype = -1, InputArray mask = noArray())

参数如下：

src：输入数组；
dst：与输入数组一样大的输出数组；
alpha：范数值，在范围归一化的情况下归一化到或较低的范围边界，即下限。
beta：在范围归一化的情况下的上范围边界，即上限；它不用于范数归一化，只用于NORM_MINMAX中。
norm_type：规范化选择的公式类型类型。
dtype：如果为负，则输出在大小、深度、通道数都等于输入；否则，它具有与src相同的通道数，深度不同，深度=CV_MAT_DEPTH。
mask：掩码。选择感兴趣区域，选定后只能对该区域进行操作。

而归一化选择的数学公式（norm_type）有，设数组元素为 $A_1，…，A_n$ ：

NORM_L1

P = \frac {A_i} {\sum A_i}\times alpha

NORM_INF

P = \frac {A_i} {\max A_i}\times alpha

NORM_L2

P = \frac {A_k} {\sqrt {A_i^2} }\times alpha

NORM_MINMAX： $A_K\notin{\max A_i},\min A_i。当A_K等于\max A_i时，p=1；当A_k等于\min A_i时，p=0$

P = \frac {A_k} {\max A_i - \min A_i}\times \vert{alpha - beta}\vert + min(alpha, beta)

同时需要注意的是alpha和beta的取值顺序与归一化结果无关。即alpha=255，beta=0和alpha=0，beta=255最后的归一化结果是相同的。

与之相关还有一个函数，其常用于将CV_16S、CV_32F等其他类型的输出图像转变成CV_8U型的图像：

1	void convertScaleAbs(InputArray src, OutputArray dst, double alpha = 1, double beta = 0)

参数如下：

src：输入数组。
dst：输出数组。
alpha：可选比例系数。
beta：添加到缩放值的可选增量，即偏移量。

该函数也可用于对整个图像数组中的每一个元素进图像增强等相关先行操作的快速运算：

dst_i = saturate_{uchar}(\vert alpha\times src_i + beta \vert)

进行 $s = T(r) = 4\log(1 + r)$ 的代码：

#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat output_image, image_gray;
    cv::cvtColor(image, image_gray, cv::COLOR_BGR2GRAY);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image_gray);

    output_image = image_gray.clone();

    for (int i = 0; i < image_gray.rows; ++ i)
        for (int j = 0; j < image_gray.cols; ++ j)
            output_image.at<uchar>(i, j) = 4 * log((double) image_gray.at<uchar>(i, j)) + 1;

    // 图像归一化，将数值变回0~255
    cv::normalize(output_image, output_image, 0, 255, cv::NORM_MINMAX);
    // 将数据类型变回CV_8U，似乎忽略此句也可
    cv::convertScaleAbs(output_image, output_image);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", output_image); 
    cv::waitKey(0);

    return 0;
}

效果展示：

3.4 幂律（伽马变换）

伽马变换：与对数函数变换类似。

s = T(r) = c\times r^γ

进行 $s = T(r) = 4\times r^{0.9}$ 代码：

#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat output_image, image_gray;
    cv::cvtColor(image, image_gray, cv::COLOR_BGR2GRAY);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image_gray);

    output_image = image_gray.clone();

    for (int i = 0; i < image_gray.rows; ++ i)
        for (int j = 0; j < image_gray.cols; ++ j)
            output_image.at<uchar>(i, j) = 4 * pow((double)image_gray.at<uchar>(i, j), 0.9);

    cv::normalize(output_image, output_image, 0, 255, cv::NORM_MINMAX);
    cv::convertScaleAbs(output_image, output_image);
    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", output_image);

    cv::waitKey(0);

    return 0;
}

效果展示：

四、直方图处理

4.1 图像直方图

非归一化直方图：

h(r_k) = n_k，其中r_k为图像像素灰度值，n_k为图像中灰度值r_k对应的像素个数

归一化直方图：

p(r_k) = \frac {n_k} {MN}，其中M和N为图像行数和列数。

计算直方图与一些函数相关：

void calcHist( const Mat* images, int nimages, const int* channels, InputArray mask,  OutputArray hist, int dims, const int* histSize, const float** ranges, bool uniform = true, bool accumulate = false )

参数如下：

images：源数组指针，它们都应该具有相同的深度，CV_8U, CV_16U或CV_32F，以及相同的大小。它们中的每一个都可以有任意数量的通道。
nimages：源图像的数量。
channels：需要统计直方图的第几通道。通道的数量必须与直方图的维度相匹配。第一个数组通道的编号从0到images[0].channels()-1，第二个数组通道的编号从images[0].channels()到images[0].channels() + images[1].channels()-1，以此类推。
mask：掩码。选择感兴趣区域，选定后只能对该区域进行操作。
hist：直方图计算的输出值。
dims：输出直方图的维度（由channels指定）。
histSize：直方图中每个dims维度需要分成多少个区间（直方图竖条的个数）。
ranges：统计像素值的区间。
uniform=true：是否对得到的直方图进行归一化处理。
accumulate=false：在多个图像时是否累计计算像素值的个数。

获取图像的直方图代码：

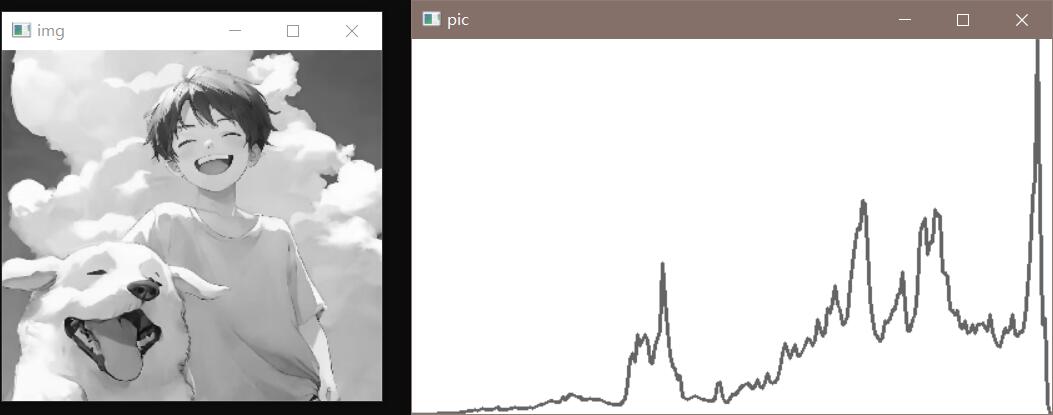
#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat hist, image_gray;
    cv::cvtColor(image, image_gray, cv::COLOR_BGR2GRAY);

    cv::namedWindow("img", cv::WINDOW_NORMAL);
    cv::imshow("img", image_gray);

    int hsize = 256;    // 直方图区间数
    float ranges[] = { 0, 256 };   // 统计像素值的区间
    const float *hRanges = { ranges };
    // 计算直方图的输出值
    cv::calcHist(&image_gray, 1, 0, cv::Mat(), hist, 1, &hsize, &hRanges, true, false);

    int hist_h = 300, hist_w = 512; // 直方图图像高和宽
    int bin_w = hist_w / hsize; // 区间

    // 直方图图像
    cv::Mat histImage(hist_h, hist_w, CV_8UC3, cv::Scalar(255, 255, 255));
    // 直方图输出值归一化到0~255
    cv::normalize(hist, hist, 0, hist_h, cv::NORM_MINMAX, -1, cv::Mat());

    for (int i = 1; i < hsize; i ++)
        cv::line(histImage, cv::Point((i - 1) * bin_w, hist_h - cvRound(hist.at<float>(i - 1))), cv::Point((i) *bin_w, hist_h - cvRound(hist.at<float>(i))), cv::Scalar(100, 100, 100), 2);

    cv::imshow("pic", histImage);
    cv::waitKey(0);
    return 0;
}

效果展示：

4.2 直方图均衡化

通过均衡化处理可以使得图像的直方图分布变得较广较平均。

经过公式：

s_k = (L - 1)\sum_{j=0}^kP_r(r_j)，k = 0,1…,L-1

其中， $s_k$ 是变换后的灰度级， $P_r(r_j)$ 是灰度级为 $r_j$ 的直方图值。

涉及一个函数：

1	void equalizeHist( InputArray src, OutputArray dst )

该函数参数十分简单，只有输入图像矩阵和输出图像矩阵，即可进行图像直方图的均衡化。

代码：

#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat hist, hist1, image_gray, image_;
    cv::cvtColor(image, image_gray, cv::COLOR_BGR2GRAY);

    cv::namedWindow("img_before", cv::WINDOW_NORMAL);
    cv::namedWindow("img_after", cv::WINDOW_NORMAL);
    cv::imshow("img_before", image_gray);

    // 直方图均衡化
    cv::equalizeHist(image_gray, image_);
    cv::imshow("img_after", image_);

    int hsize = 256;    // 直方图区间数
    float ranges[] = { 0, 256 };   // 统计像素值的区间
    const float *hRanges = { ranges };
    // 计算直方图的输出值
    cv::calcHist(&image_gray, 1, 0, cv::Mat(), hist, 1, &hsize, &hRanges, true, false);
    cv::calcHist(&image_, 1, 0, cv::Mat(), hist1, 1, &hsize, &hRanges, true, false);

    int hist_h = 300, hist_w = 512; // 直方图图像高和宽
    int bin_w = hist_w / hsize; // 区间

    // 直方图图像
    cv::Mat histImage(hist_h, hist_w, CV_8UC3, cv::Scalar(255, 255, 255));
    cv::Mat histImage1(hist_h, hist_w, CV_8UC3, cv::Scalar(255, 255, 255));

    // 直方图输出值归一化到0~255
    cv::normalize(hist, hist, 0, hist_h, cv::NORM_MINMAX, -1, cv::Mat());
    cv::normalize(hist1, hist1, 0, hist_h, cv::NORM_MINMAX, -1, cv::Mat());

    for (int i = 1; i < hsize; i ++)
    {
        cv::line(histImage, cv::Point((i - 1) * bin_w, hist_h - cvRound(hist.at<float>(i - 1))), cv::Point((i) *bin_w, hist_h - cvRound(hist.at<float>(i))), cv::Scalar(100, 100, 100), 2);
        cv::line(histImage1, cv::Point((i - 1) * bin_w, hist_h - cvRound(hist1.at<float>(i - 1))), cv::Point((i) *bin_w, hist_h - cvRound(hist1.at<float>(i))), cv::Scalar(100, 100, 100), 2);
    }

    cv::imshow("before", histImage);
    cv::imshow("after", histImage1);
    cv::waitKey(0);
    return 0;
}

效果展示：

4.3 直方图匹配

将需要处理的图像匹配另一幅直方图形状。

由于直方图均衡化映射函数T为单调递增，即变换后的直方图可以经过逆变换回到原直方图。

得到直方图匹配的步骤：

计算输入图像的直方图 $P(r)$ ，并进行直方图均衡化，得到均衡化后的灰度 $s_k$ 。
根据公式计算 $G(z_q)$ 并存储。

G(z_q) = (L - 1)\sum_{i = 0}^qP_z(z_j)

对 $s_k$ 的每个值，都找到 $z_q$ 对应的值，使得 $G(z_q)$ 最接近 $s_k$ ，并存储从s到z的映射。
从步骤3中找到映射，将 $s_k$ 的值映射到直方图指定图像中值为 $z_q$ 的对应像素，形成直方图。

涉及映射Look up Table（LUT）函数：

1	void LUT(InputArray src, InputArray lut, OutputArray dst)

参数如下：

src：表示输入图像。
lut：表示查找表。
dst：表示输出图像。

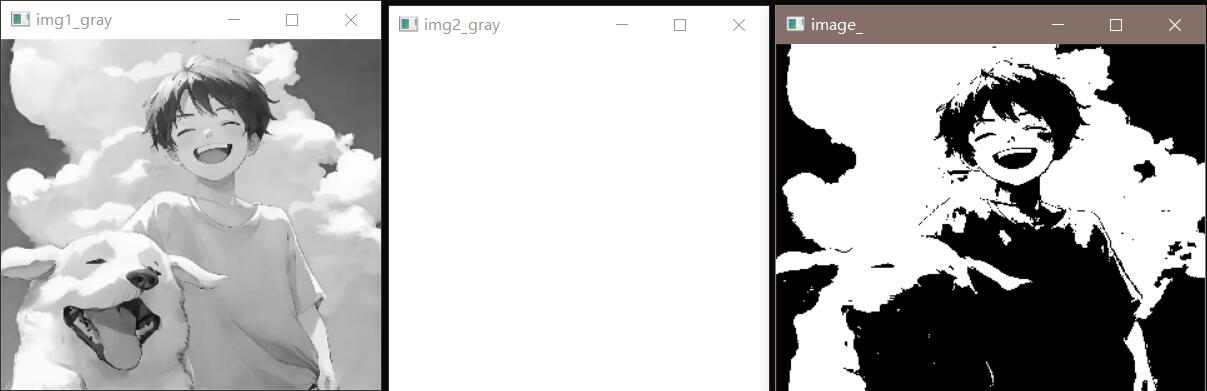
代码：white.jpg为纯白图像

#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat image1 = cv::imread("src/test.jpg"), image2 = cv::imread("src/white.jpg");
    cv::Mat image1_gray, image2_gray, hist1, hist2, image_;
    cv::cvtColor(image1, image1_gray, cv::COLOR_BGR2GRAY);
    cv::cvtColor(image2, image2_gray, cv::COLOR_BGR2GRAY);
    cv::namedWindow("img1_gray", cv::WINDOW_NORMAL);
    cv::namedWindow("img2_gray", cv::WINDOW_NORMAL);
    cv::imshow("img1_gray", image1_gray);
    cv::imshow("img2_gray", image2_gray);

    // 图像1和图像2进行均衡化
    cv::equalizeHist(image1_gray, image1_gray);
    cv::equalizeHist(image2_gray, image2_gray);

    // 求图像1和图像2均衡化后的直方图
    int hsize = 256;
    float ranges[] = { 0, 256 };
    const float *hranges = { ranges };
    cv::calcHist(&image1_gray, 1, 0, cv::Mat(), hist1, 1, &hsize, &hranges, true, false);
    cv::calcHist(&image2_gray, 1, 0, cv::Mat(), hist2, 1, &hsize, &hranges, true, false);

    // 计算两个均衡化图像直方图的累积概率
    float hist1_rate[256] = { hist1.at<float>(0) };
    float hist2_rate[256] = { hist2.at<float>(0) };
    for (int i = 1; i < 256; i ++)
    {
        hist1_rate[i] = (hist1_rate[i - 1] + hist1.at<float>(i));
        hist2_rate[i] = (hist2_rate[i - 1] + hist2.at<float>(i));
    }

    for (int i = 0; i < 256; i ++)
    {
        hist1_rate[i] /= (image1_gray.rows * image1_gray.cols);
        hist2_rate[i] /= (image2_gray.rows * image2_gray.cols);
    }

    // 两个累计概率之间的差值，用于找到最接近的点
    float diff[256][256];
    for (int i = 0; i < 256; i ++)
        for (int j = 0; j < 256; j ++)
            diff[i][j] = fabs(hist1_rate[i] - hist2_rate[j]);

    cv::Mat lut(1, 256, CV_8U);
    for (int i = 0; i < 256; i ++)
    {
        // 查找源灰度级为i的映射灰度和i的累积概率差最小(灰度接近)的规定化灰度
        float min = diff[i][0];
        int idx = 0;
        for (int j = 0; j < 256; j ++)
        {
            if(min > diff[i][j])
            {
                min = diff[i][j];
                idx = j;
            }
        }
        lut.at<uchar>(i) = idx;
    }
    cv::LUT(image1_gray, lut, image_);
    cv::namedWindow("image_", cv::WINDOW_NORMAL);
    cv::imshow("image_", image_);

    cv::waitKey(0);
    return 0;
}

效果展示：

五、空间滤波基础

讨论使用空间滤波器进行图像处理。

5.1 线性空间滤波

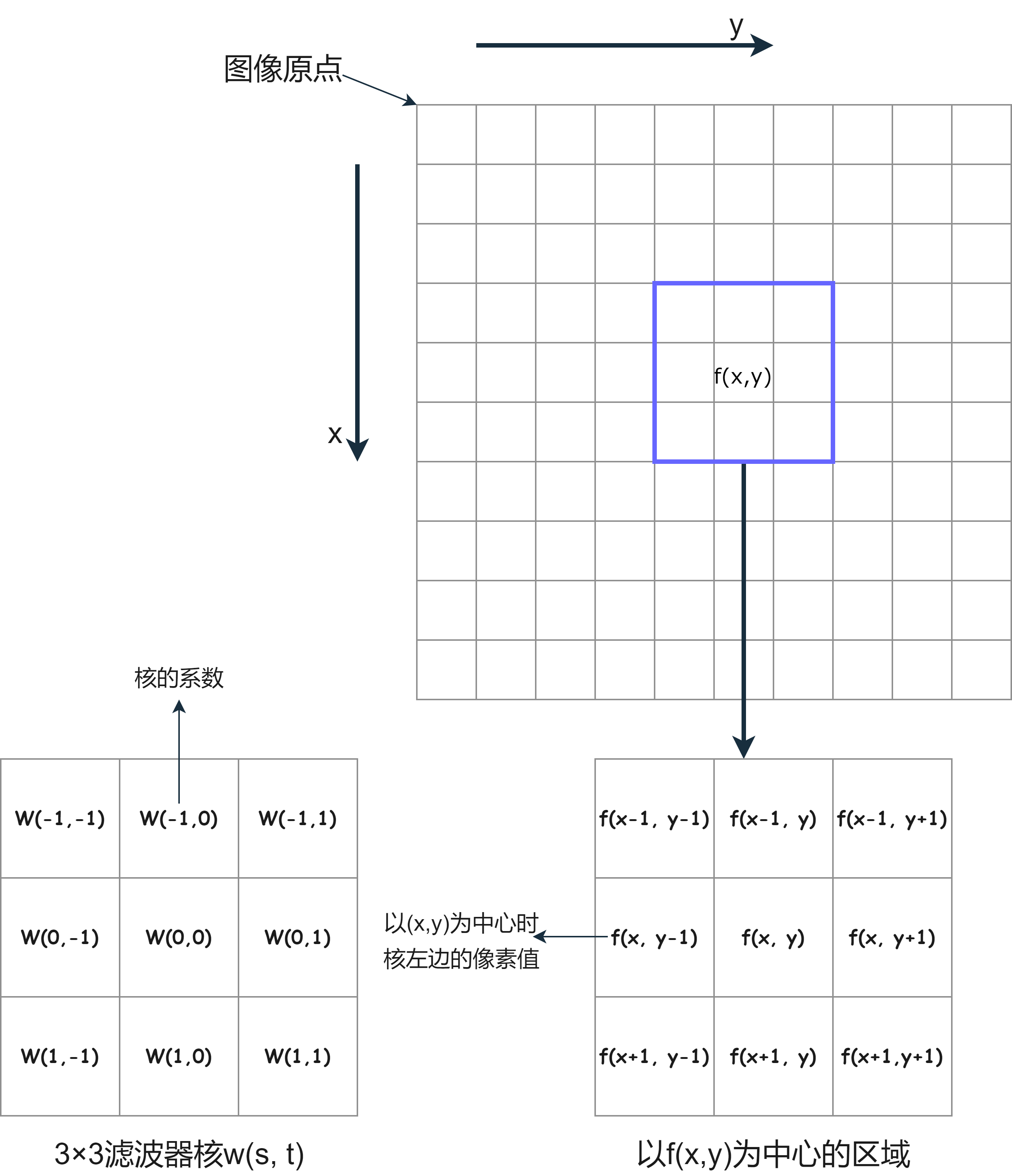
线性空间滤波器在图像f和滤波器核w之间执行乘积之和运算。

滤波器核（或称核）是一个阵列，其大小定义了运算的邻域，其系数决定了该滤波器的性质。

在上图的任何一点(x, y)处，滤波器的响应g(x, y)是核系数与核所覆盖图像像素的乘积之和：

g(x,y) = w(-1,-1)f(x-1,y-1)+w(-1,0)f(x-1,y)+…+w(1,1)f(x+1, y+1)

坐标x和y变化时，核的中心逐个像素移动，并在移动过程中生成了滤波后的图像g。

核中心系数w(0,0)对其于(x,y)处的像素，当大小为m×n的核，假设m=2a+1，n=2b+1，a和b非负。这意味着这是两个坐标方向上奇数大小的核。

一般而言，大小为m×n的核对大小为M×N的图像的线性空间滤波可以表示为：

g(x,y) = \sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)

在上式中，x和y发生变化时，核的原点可以访问图像的每个像素。当x和y不变时，上式即乘积之和，只适合任意奇数大小的核。

5.2 空间相关与卷积

对于式子：

g(x,y) = \sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)

化简为一维讨论：

g(x) = \sum_{s=-a}^aw(s)f(x+s)

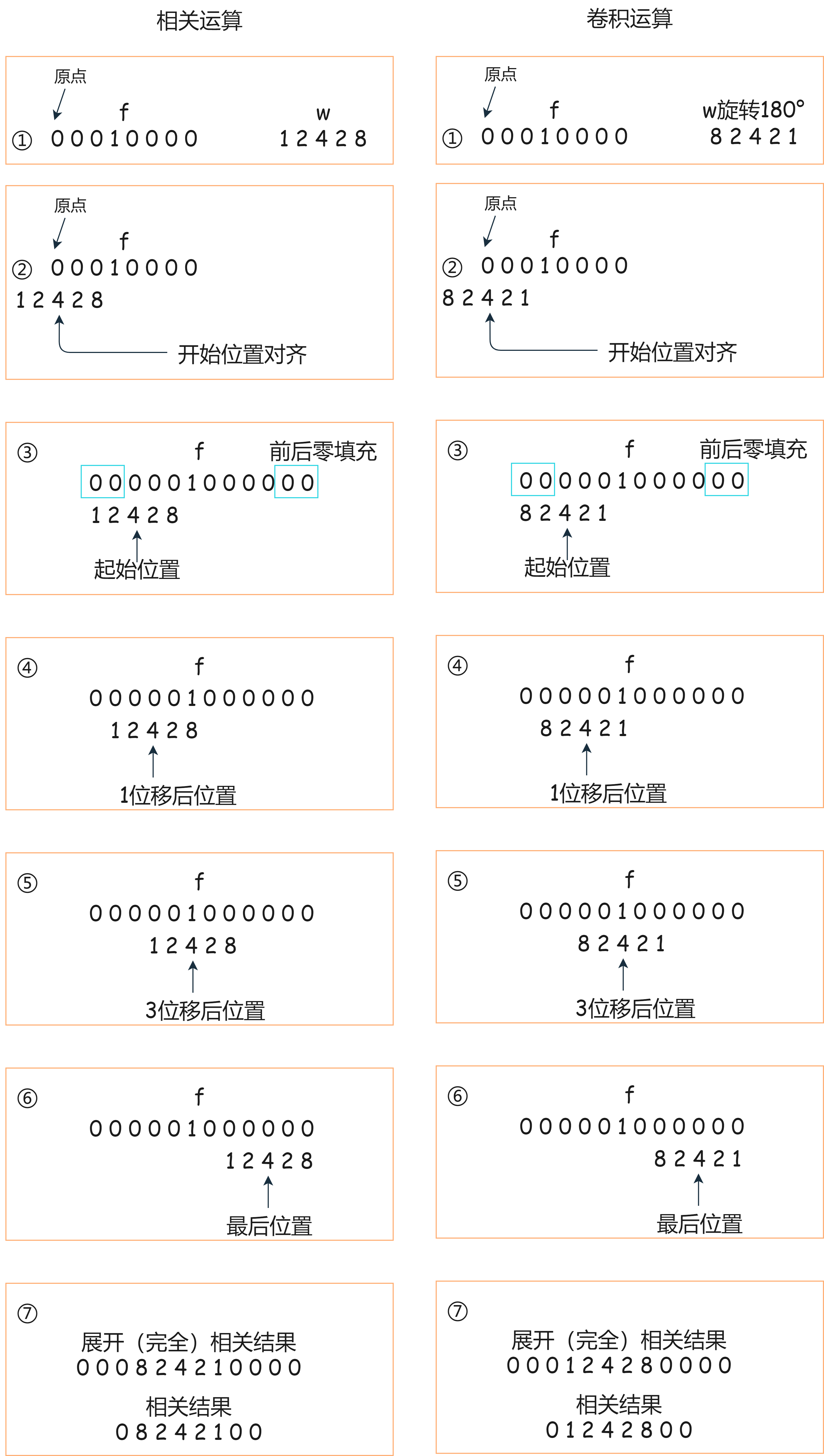
举一个一维例子：核w为 1 2 4 2 8

相关是滤波器核相对于图像的位移的函数，即相关的第一个值对应于核的零位移，第二个值对应于核的1单位位移。

卷积是滤波器核先进行预旋转，再进行相对于图像位移的函数。

①该核大小为 $1\times 5$ ，那么有a=2，b=0。

②w中心系数要与f的原点重合。

③w的一部分在f之外，求和不能运算，所以进行零补充（零补充不是唯一选择）。如果核大小为1×m，那么在两侧都需要补 $(m-1)/2$ 个0。

接下来根据移动和式计算：

g(x) = \sum_{s=-a}^aw(s)f(x+s)\\ g(0) = \sum_{s=-2}^2w(s)f(s+0) = 0\\ g(1) = \sum_{s=-2}^2w(s)f(s+1) = 8\\ g(2) = \sum_{s=-2}^2w(s)f(s+2) = 2\\ g(3) = \sum_{s=-2}^2w(s)f(s+3) = 4\\ g(4) = \sum_{s=-2}^2w(s)f(s+4) = 2\\ g(5) = \sum_{s=-2}^2w(s)f(s+5) = 1\\ g(6) = \sum_{s=-2}^2w(s)f(s+6) = 0\\ g(7) = \sum_{s=-2}^2w(s)f(s+7) = 0\\

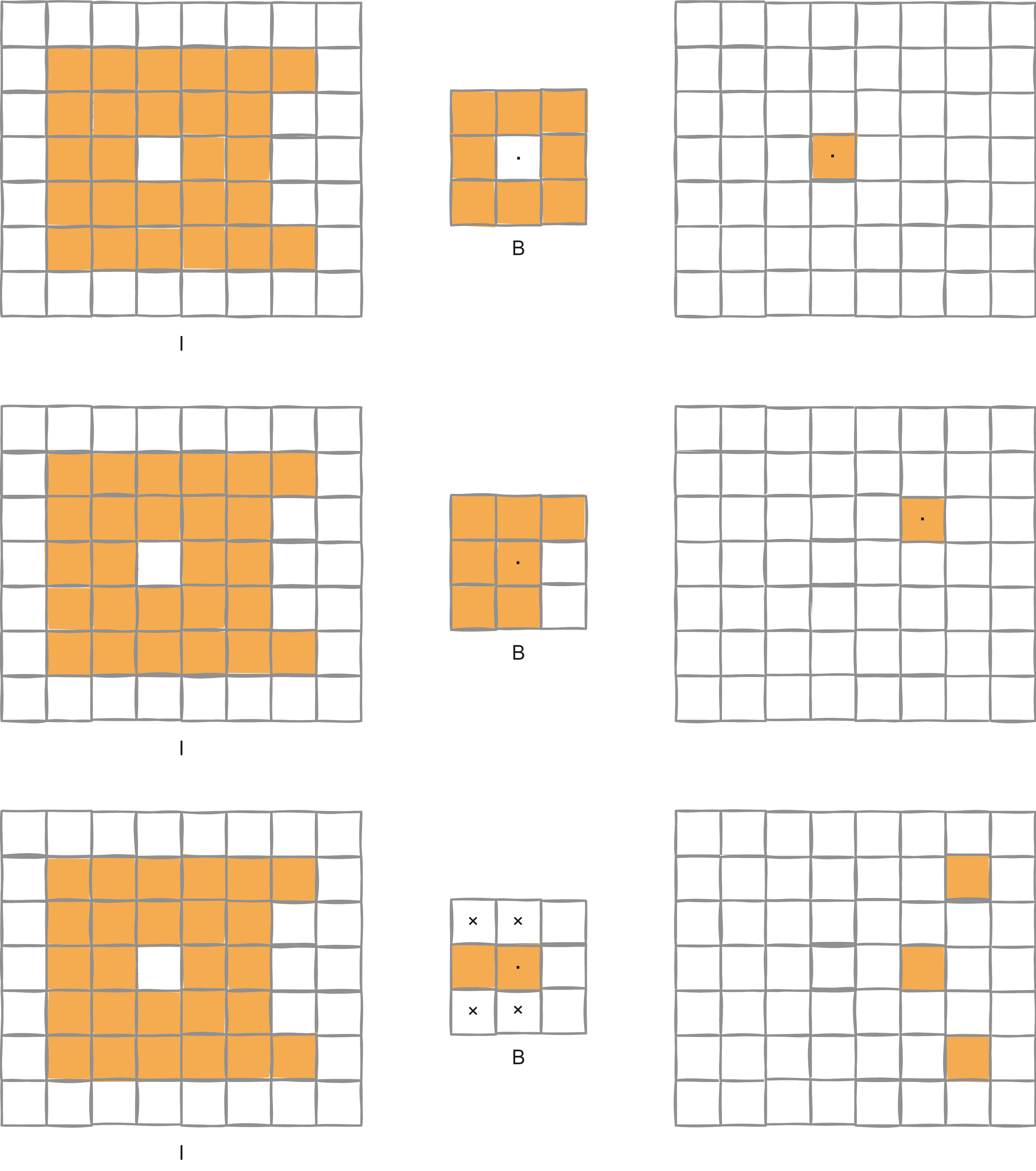
另外，把一个元素是1，其余元素是0的函数称为 离散单位冲激函数。而核与离散单位冲激函数进行相关时，会在这个冲激的位置产生核的旋转版本。

广泛地说，一个函数与一个冲激进行卷积时，在冲激所在的位置产生这个函数的副本。

将一维推广到二维图像，对于大小为m×n的核，需要在图像的顶部核底部至少补 $(m-1)/2$ 行0，在左侧和右侧至少补 $(n-1)/2$ 列0。

假设m和n都为3：

二维下的旋转180°等效于核关于其一个轴旋转，再关于另一个轴旋转。

回头再看冲激函数，其坐标 $(x_0,y_0)$ 处的离散冲激强度（振幅）A定义为：

δ(x-x_0,y-y_0)=\left\{ \begin{matrix} A,&x_0=x和y_0=y\\ 0,&其他 \end{matrix} \right.

小结

大小为m×n的核w与图像f(x,y)的相关：

w☆f(x,y)=(w☆f)(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)

大小为m×n的核w与图像f(x,y)的卷积：

w★f(x,y)=(w★f)(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x-s,y-t)

当卷积其中的一个函数旋转180°后，减号对应其f和w的坐标，也可以完成乘积之和处理即线性空间滤波。

相关和卷积运算满足的性质：

性质	卷积	相关
交换律	f★g = g★f	不成立
结合律	f★(g★h) = (f★g)★h	不成立
分配律	f★(g+h)=(f★g)+(f★h)	f☆(g+h)=(f☆g)+(f☆h)

5.3 低通空间滤波器

5.3.1 盒式滤波器、均值滤波器

均值滤波就是将区域内的像素灰度值的平均值作为中心像素的灰度值。

一个3×3的均值滤波器核如：

\qquad 1\qquad1\qquad1\\ \frac 19\times 1\qquad 1\qquad1\\ \qquad 1\qquad1\qquad1

OpenCV提供了一个均值滤波（盒式滤波器）函数；

1	void blur(InputArray src, OutputArray dst, Size ksize, Point anchor = Point(-1,-1), int borderType = BORDER_DEFAULT)

参数如下：

src：输入图像; 它可以有任意数量的通道，这些通道是独立处理的，但深度应该是CV_8U, CV_16U, CV_16S, CV_32F或CV_64F。
dst：输出与src相同大小和类型的图像。
ksize：核大小，cv::Size类型。
anchor：锚点，默认值Point(-1，-1)表示锚点位于内核中心。
borderType：int类型，用于推断图像外部像素的某种边界模式，一般不管。

代码：

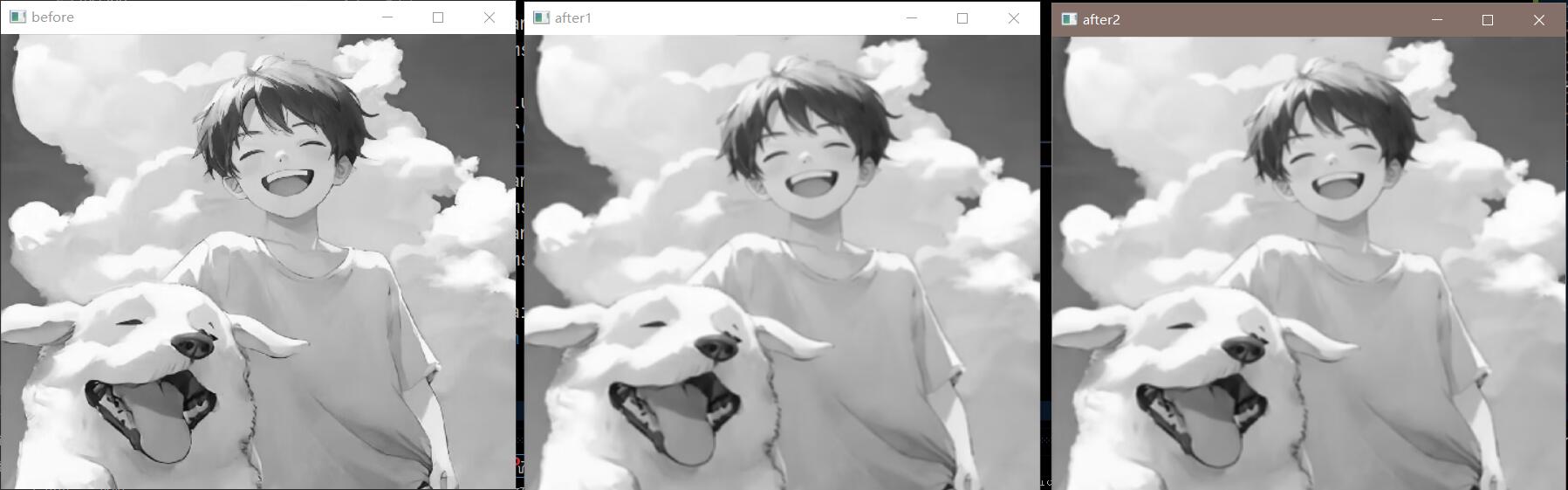
#include <opencv2/opencv.hpp>
#include <iostream>

// 手动实现盒式均值滤波器
void filter(int filter_size, cv::Mat &image_input, cv::Mat &image_output)
{
    image_output = image_input.clone();
    int k = (filter_size - 1) / 2;  // 实现对齐核中心元素
    for (int i = k; i < image_input.rows - k; i ++)
    {
        for (int j = k; j < image_input.cols - k; j ++)
        {
            int sum = 0;    // 计算相关
            for (int m = -k; m < k + 1; m ++)
                for (int n = -k; n < k + 1; n ++)
                    sum += image_input.at<uchar>(i + m, j + n);

            image_output.at<uchar>(i, j) = round(sum / (filter_size * filter_size));
        }
    }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg", 0);
    cv::Mat image_output, image_output2;

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    // CV自带的均值滤波器，核大小为7
    cv::blur(image, image_output, cv::Size(7, 7));
    // 自己实现的均值滤波器，核大小为7
    filter(7, image, image_output2);

    // 对比CV自带的均值滤波器与自己实现的均值滤波器性能表现
    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

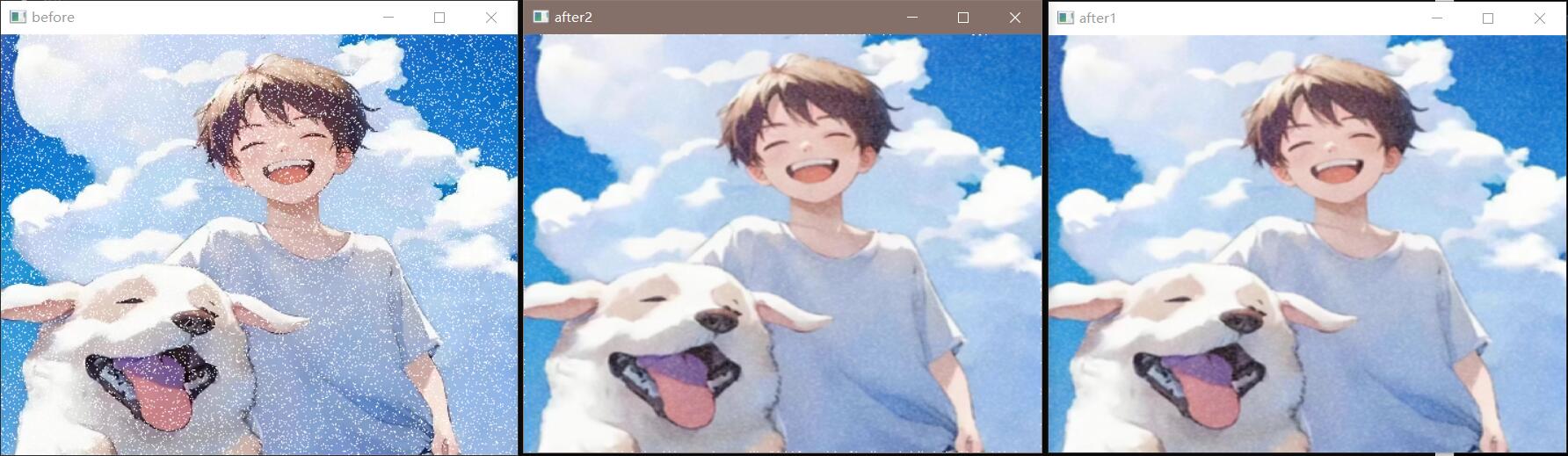
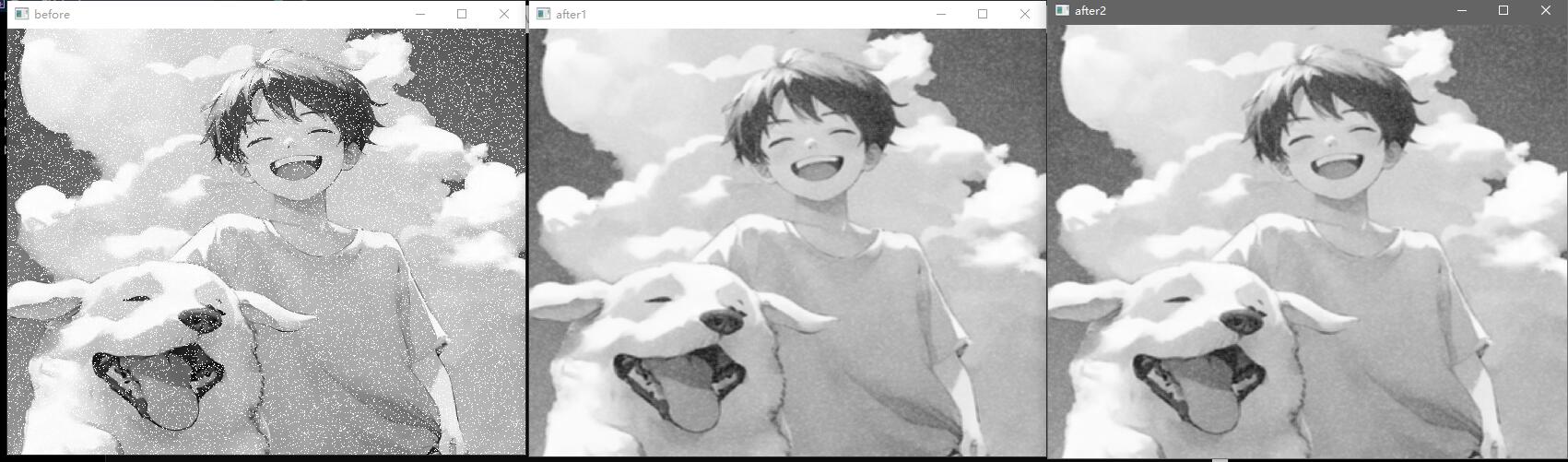
也许上述效果不明显，可以进行彩色图像，增加杂波，再进行均值滤波器处理。

代码：

#include <opencv2/opencv.hpp>
#include <iostream>
#include <random>

// 随机将n个像素值变成白点，构成噪声
void Salt(cv::Mat image, int n)
{
    // 生成随机数
    std::default_random_engine generater;
    std::uniform_int_distribution<int>randomRow(0, image.rows - 1);
    std::uniform_int_distribution<int>randomCol(0, image.cols - 1);

    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = randomRow(generater);
        j = randomCol(generater);
        if (image.channels() == 1)
            image.at<uchar>(i, j) = 255;
        if (image.channels() == 3)
        {
            image.at<cv::Vec3b>(i, j)[0] = 255;
            image.at<cv::Vec3b>(i, j)[1] = 255;
            image.at<cv::Vec3b>(i, j)[2] = 255;
        }
    }
}

// 手动实现均值滤波器，BGR三通道都进行均值滤波
void filter(int filter_size, cv::Mat &image_input, cv::Mat &image_output)
{
    image_output = image_input.clone();
    int k = (filter_size - 1) / 2;
    for (int i = k; i < image_input.rows - k; i ++)
    {
        for (int j = k; j < image_input.cols - k; j ++)
        {
            int sum1 = 0, sum2 = 0, sum3 = 0;
            for (int m = -k; m < k + 1; m ++)
            {
                for (int n = -k; n < k + 1; n ++)
                {
                    sum1 += image_input.at<cv::Vec3b>(i + m, j + n)[0];
                    sum2 += image_input.at<cv::Vec3b>(i + m, j + n)[1];
                    sum3 += image_input.at<cv::Vec3b>(i + m, j + n)[2];
                }

            }
            image_output.at<cv::Vec3b>(i, j)[0] = round(sum1 / (filter_size * filter_size));
            image_output.at<cv::Vec3b>(i, j)[1] = round(sum2 / (filter_size * filter_size));
            image_output.at<cv::Vec3b>(i, j)[2] = round(sum3 / (filter_size * filter_size));
        }
    }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat image_output, image_output2;
    Salt(image, 100000);    // 随机生成10w个白点构成噪声

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    cv::blur(image, image_output, cv::Size(7, 7));
    filter(7, image, image_output2);

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

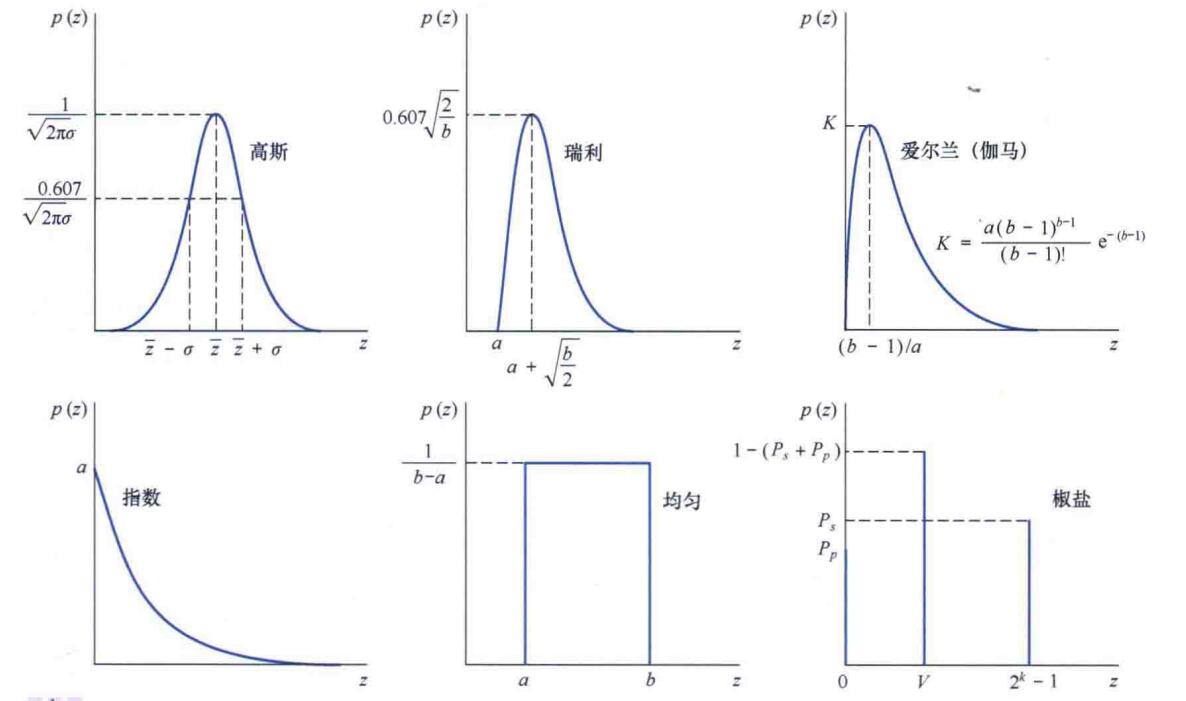
5.3.2 高斯滤波器

在统计学与概率论中，高斯函数是正态分布（高斯分布）的密度函数。一维的高斯表达式如下：

f(x)=ae^{-\frac{(x-μ)^2} {2σ^2} }\\

其中a、μ、σ为实数常数，a>0；a表示曲线的高度，μ表示曲线在x轴的中心，σ与半峰全宽有关。

而二维高斯表达式如下：

G(x,y)=\frac{1} {2\piσ^2}e^{-\frac{-(x^2+y^2)} {2σ^2} }

故高斯核为：

w(s,t)=G(s,t)=Ke^{-\frac{s^2+t^2} {2σ^2} }\\ G(r)=Ke^{-\frac{r^2} {2σ^2} }，当r=(s^2+t^2)^{\frac 12}

OpenCV提供了一个高斯滤波器函数；

1	void GaussianBlur( InputArray src, OutputArray dst, Size ksize, double sigmaX, double sigmaY = 0, int borderType = BORDER_DEFAULT )

参数如下：

src：输入图像; 它可以有任意数量的通道，这些通道是独立处理的，但深度应该是CV_8U, CV_16U, CV_16S, CV_32F或CV_64F。
dst：输出与src相同大小和类型的图像。
ksize：核大小，cv::Size类型。
sigmaX：高斯核函数在X方向上的标准偏差。
sigmaY：高斯核函数在Y方向上的标准偏差。如果sigmaY为0，则将其设为sigmaX；如果sigmaX核sigmaY都为0，则有ksize.width核ksize.height计算。
borderType：int类型，用于推断图像外部像素的某种边界模式，一般不管。

代码：

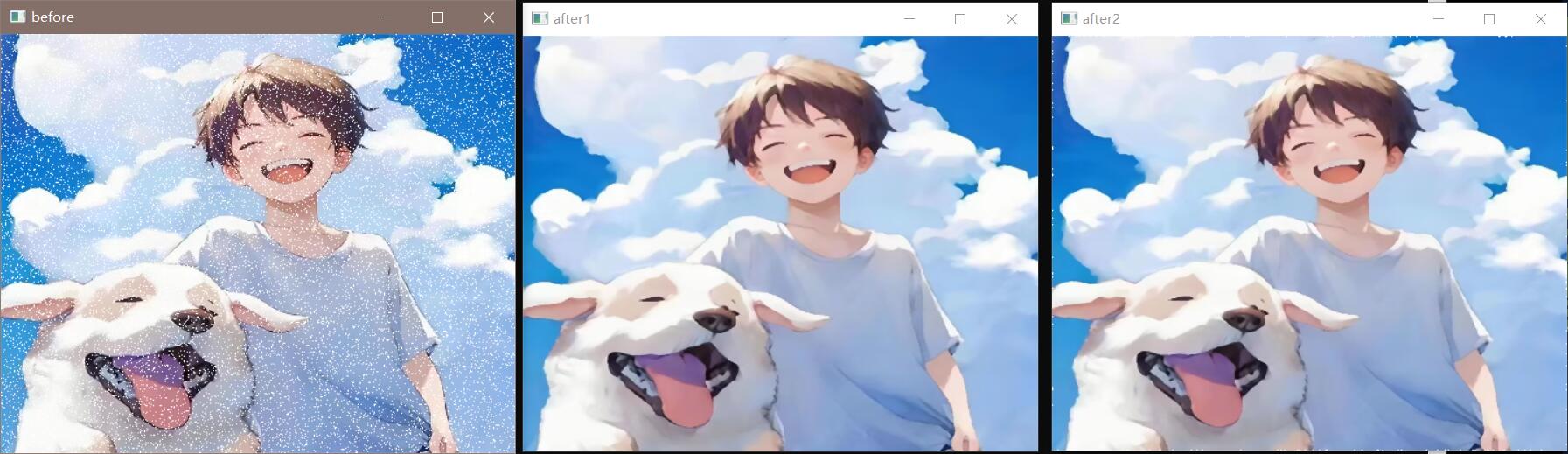
#include <opencv2/opencv.hpp>
#include <iostream>
#include <random>
#include <cmath>

// 随机将n个像素值变成白点，构成噪声
void Salt(cv::Mat image, int n)
{
    // 生成随机数
    std::default_random_engine generater;
    std::uniform_int_distribution<int>randomRow(0, image.rows - 1);
    std::uniform_int_distribution<int>randomCol(0, image.cols - 1);

    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = randomRow(generater);
        j = randomCol(generater);
        if (image.channels() == 1)
            image.at<uchar>(i, j) = 255;
        if (image.channels() == 3)
        {
            image.at<cv::Vec3b>(i, j)[0] = 255;
            image.at<cv::Vec3b>(i, j)[1] = 255;
            image.at<cv::Vec3b>(i, j)[2] = 255;
        }
    }
}

// 手动实现高斯滤波器，BGR三通道都进行高斯滤波
void filter1(int filter_size, cv::Mat &image_input, cv::Mat &image_output)
{
    image_output = image_input.clone();
    int k = (filter_size - 1) / 2;
    for (int i = k; i < image_input.rows - k; i ++)
    {
        for (int j = k; j < image_input.cols - k; j ++)
        {
            double sum1 = 0.0, sum2 = 0.0, sum3 = 0.0;
            double sum1_ = 0.0, sum2_ = 0.0, sum3_ = 0.0;
            double sigma = 7, g;   // sigma可修改
            for (int m = -k; m < k + 1; m ++)
            {
                for (int n = -k; n < k + 1; n ++)
                {
                    g = exp(-(m * m + n * n) / (2 * sigma * sigma));
                    sum1 += g * image_input.at<cv::Vec3b>(i + m, j + n)[0];
                    sum1_ += g;
                    sum2 += g * image_input.at<cv::Vec3b>(i + m, j + n)[1];
                    sum2_ += g;
                    sum3 += g * image_input.at<cv::Vec3b>(i + m, j + n)[2];
                    sum3_ += g;
                }

            }
            image_output.at<cv::Vec3b>(i, j)[0] = (int) round(sum1 / sum1_);
            image_output.at<cv::Vec3b>(i, j)[1] = (int) round(sum2 / sum2_);
            image_output.at<cv::Vec3b>(i, j)[2] = (int) round(sum3 / sum3_);
        }
    }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat image_output, image_output2;
    Salt(image, 100000);    // 随机生成10w个白点构成噪声

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    cv::GaussianBlur(image, image_output, cv::Size(7, 7), 2, 2);
    filter1(7, image, image_output2);

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

5.3.3 中值滤波

中值滤波就是取周围邻域像素灰度值（或GRB值）的中值作为中心像素灰度值结果。

OpenCV提供了一个中值滤波器函数；

1	void medianBlur(InputArray src, OutputArray dst, int ksize)

参数如下：

src：输入图像; 输入1、3或4通道图像，当ksize为3或5时，图像深度应该是CV_8U、CV_16U或CV_32F，对于更大的孔径尺寸，只能是CV_8U。
dst：输出与src相同大小和类型的图像。
ksize：核大小。

代码：

#include <opencv2/opencv.hpp>
#include <iostream>
#include <random>
#include <cmath>

// 随机将n个像素值变成白点，构成噪声
void Salt(cv::Mat image, int n)
{
    // 生成随机数
    std::default_random_engine generater;
    std::uniform_int_distribution<int>randomRow(0, image.rows - 1);
    std::uniform_int_distribution<int>randomCol(0, image.cols - 1);

    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = randomRow(generater);
        j = randomCol(generater);
        if (image.channels() == 1)
            image.at<uchar>(i, j) = 255;
        if (image.channels() == 3)
        {
            image.at<cv::Vec3b>(i, j)[0] = 255;
            image.at<cv::Vec3b>(i, j)[1] = 255;
            image.at<cv::Vec3b>(i, j)[2] = 255;
        }
    }
}

// 找中值
cv::Vec3b MedianFinding(cv::Mat &mat, int filter_size)
{
    cv::Vec3b tmp;
    cv::Vec3b m;
    for (int i = 1; i <= filter_size - 1; i++)
    {
        for (int j = 1; j <= filter_size - i; j++)
        {
            if (mat.at<cv::Vec3b>(j - 1)[0] > mat.at<cv::Vec3b>(j)[0])
            {
                tmp = mat.at<cv::Vec3b>(j - 1);
                mat.at<cv::Vec3b>(j - 1) = mat.at<cv::Vec3b>(j);
                mat.at<cv::Vec3b>(j) = tmp;
            }
        }
    }
    return m = mat.at<cv::Vec3b>((filter_size + 1) / 2);
}

// 手动实现中值滤波器，BGR三通道都进行中值滤波
void filter2(int filter_size, cv::Mat &image_input, cv::Mat &image_output)
{
    image_output = image_input.clone();
    int k = (filter_size - 1) / 2;
    cv::Mat arry(1, filter_size * filter_size, CV_8UC3);
    for (int i = k; i < image_input.rows - k; i ++)
    {
        for (int j = k; j < image_input.cols - k; j ++)
        {
            int mid = 0;
            for (int m = -k; m < k + 1; m ++)
            {
                for (int n = -k; n < k + 1; n ++)
                {
                    arry.at<cv::Vec3b>(mid) = image_input.at<cv::Vec3b>(i + m, j + n);
                    mid ++;
                }
            }
            image_output.at<cv::Vec3b>(i, j) = MedianFinding(arry, filter_size * filter_size);
        }
    }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat image_output, image_output2;
    Salt(image, 100000);    // 随机生成10w个白点构成噪声

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    cv::medianBlur(image, image_output, 7);
    filter2(7, image, image_output2);   // 个人体验速度较慢

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

5.4 高通空间滤波器

5.4.1 基础

锐化的作用时突出灰度中的过渡。

平滑可以类似为积分运算，那么锐化则可以类似为微分运算。图像模糊在空间域中可以通过平均（平滑）一个邻域中的像素实现。而图像微分将会增强边缘和其他不连续（如噪声）。

数字函数的导数是用差分定义，一阶导数的任何定义都要满足：

恒定灰度区域的一阶导数必须为零。
灰度台阶或斜坡开始处的一阶导数必须非零。
灰度斜坡上的一阶导数必须非零。

类似有二阶导数的任何定义都要满足：

恒定灰度区域的二阶导数必须为零。
灰度台阶或斜坡的开始处和结束处的二阶导数必须非零。
灰度斜坡上的二阶导数必须为零。

而处理图像时，变化发生的最短距离也就是像素间的距离。

一维函数 $f(x)$ 的一阶导数的一个基本定义是差分：

\frac {\mathrm{d}f} {\mathrm{d}x}=f(x+1)-f(x)

二维函数 $f(x,y)$ 的二阶导数定义为差分：

\frac {\partial^2 f} {\partial x^2}=f(x+1)+f(x-1)-2f(x)

先用一维函数举例：

一维函数导数满足上述性质，类比一维函数可知二维函数。数字图像的边缘在灰度上通常类似于斜坡过渡，图像的一阶导数会产生较宽的边缘；另外，二阶导数会产生宽度为1像素并由零分隔的双边缘。所以， 与一阶导数相比，二阶导数可增强更精细的细节，而实现二阶导数所需的运算量也更少。

5.4.2 拉普拉斯锐化滤波

最简单的各向同性导数算子（核）是拉普拉斯。 对于两个变量的函数 $f(x,y)$ ，定义为：

\nabla^2f=\frac {\partial^2f} {\partial x^2} + \frac {\partial^2f} {\partial y^2}

拉普拉斯是线性算子。在x方向有：

\frac{\partial^2f} {\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)

在y方向有：

\frac{\partial^2f} {\partial x^2}=f(x,y+1)+f(x,y-1)-2f(x,y)

由上面三个式子可得两个变量的拉普拉斯是：

\nabla^2f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)

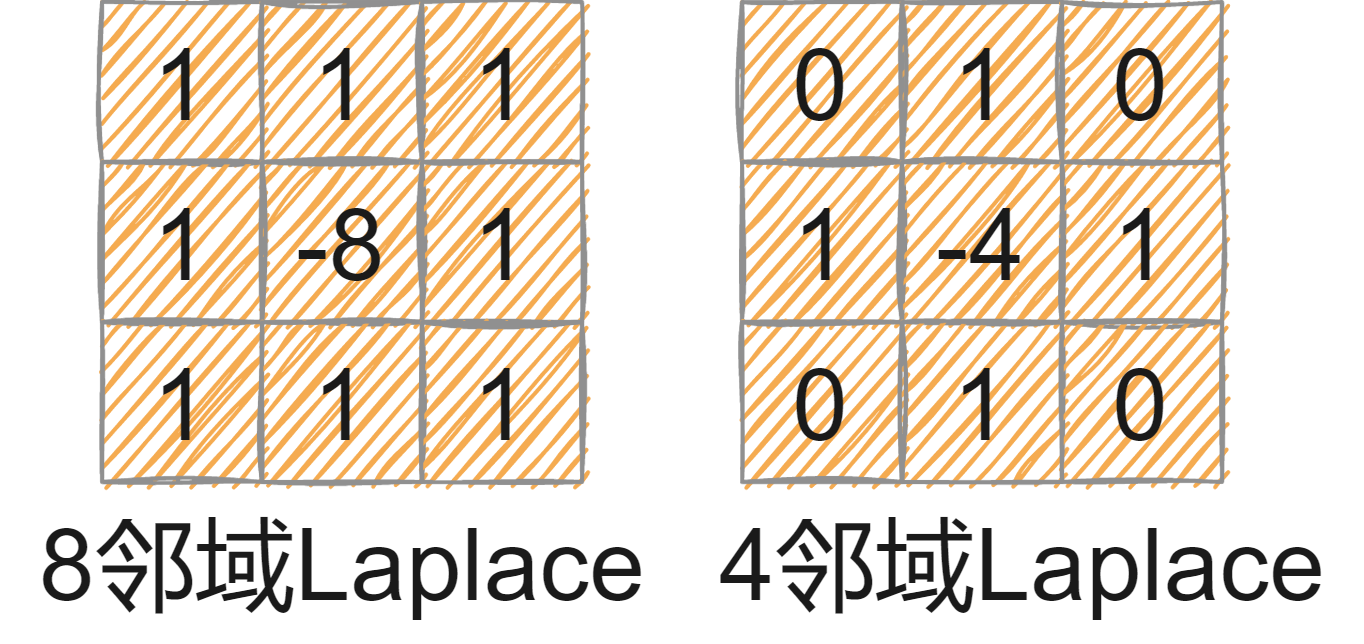
该公式可以使用卷积运算，上式的拉普拉斯核为：

0	1	0
1	-4	1
0	1	0

(a)

这个也叫四邻域核，还有八邻域核：

1	1	1
1	-8	1
1	1	1

(b)

两个其他的核（系数反转）：

0	-1	0
-1	4	-1
0	-1	0

-1	-1	-1
-1	8	-1
-1	-1	-1

(d)

但是不能直接使用拉普拉斯，它会突出图像中急剧灰度过渡，不强调缓慢变化的灰度区域，往往会产生具有灰色边缘线核其他不连续的图像。所以需要 将拉普拉斯图像和原图像相加恢复背景特征。

使用拉普拉斯锐化图像：

g(x,y)=f(x,y)+c[\nabla^2f(x,y)]

f(x,y)为输入图像，g(x,y)为锐化后图像。若使用核(a)或核(b)，取c=-1；若使用核©或核(d)，取c=1。

代码：

#include <opencv2/opencv.hpp>
#include <iostream>

// 四邻域拉普拉斯核
void filter_4(cv::Mat &input, cv::Mat &output)
{
    output = input.clone();
    int la;
    for (int i = 1; i < input.rows - 1; i ++)
        for (int j = 1; j < input.cols - 1; j ++)
        {
            la = input.at<uchar>(i + 1, j) + input.at<uchar>(i - 1, j)
                + input.at<uchar>(i, j + 1) + input.at<uchar>(i, j - 1)
                - 4 * input.at<uchar>(i, j);
            output.at<uchar>(i, j) = cv::saturate_cast<uchar>(output.at<uchar>(i, j) - la);
        }
}

// 八邻域拉普拉斯核
void filter_8(cv::Mat &input, cv::Mat &output)
{
    output = input.clone();
    int la;
    for (int i = 1; i < input.rows - 1; i ++)
        for (int j = 1; j < input.cols - 1; j ++)
        {
            la = input.at<uchar>(i - 1, j - 1) + input.at<uchar>(i - 1, j) +
                input.at<uchar>(i - 1, j + 1) + input.at<uchar>(i, j - 1) +
                input.at<uchar>(i, j + 1) + input.at<uchar>(i + 1, j - 1) +
                input.at<uchar>(i + 1, j) + input.at<uchar>(i + 1, j + 1) -
                8 * input.at<uchar>(i, j);
            output.at<uchar>(i, j) = cv::saturate_cast<uchar>(output.at<uchar>(i, j) - la);
        }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg", 0);
    cv::Mat image_output, image_output2;

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    filter_4(image, image_output);
    filter_8(image, image_output2);

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

拉普拉斯锐化滤波对于灰度图像的影响十分明显，但是对于彩色图像影响一般。如果想改为适用于彩色图像，只需将数据类型从 uchar 改为 cv::Vec2b。

效果展示：

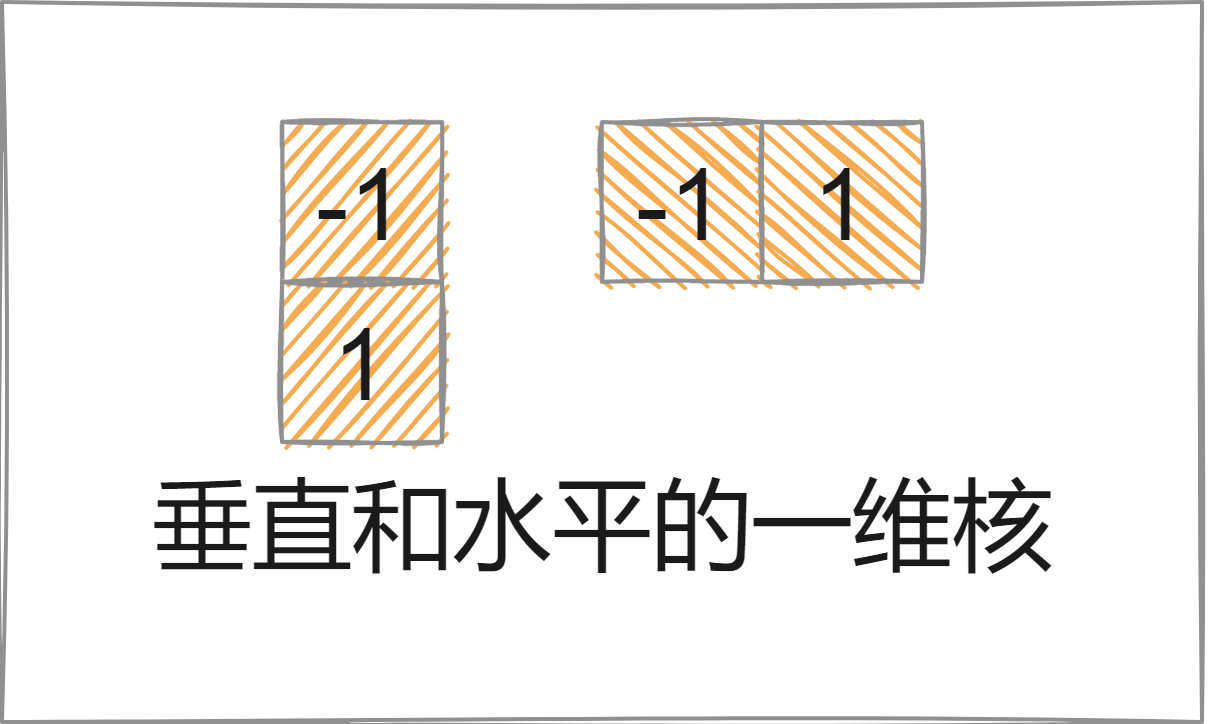
5.4.3 一阶导数锐化——梯度

一阶导数是用梯度幅度实现。图像f在坐标(x,y)处的梯度定义为二维列向量：

\nabla f\equiv grad(f)=\left[\begin{matrix}g_x \\ g_y\end{matrix}\right]=\left[\begin{matrix}\partial f/\partial x \\ \partial f/\partial y\end{matrix}\right]

这个向量指向f的最大变化率方向。

向量 $\nabla f$ 的幅度（长度）表示为M(x,y)（有时候用 $\vert\vert\nabla f\vert\vert$ ），其中

M(x,y)=\vert\vert\nabla f\vert\vert=mag(\nabla f)=\sqrt{g_x^2+g_y^2}

是梯度向量方向的变化率在(x,y)处的值，方向为：

\alpha(x,y)=\tan^{-1}\left[\begin{matrix}\frac{g_y(x,y)} {g_x(x,y)}\end{matrix}\right]

而M(x,y)是与原图像大小相同的图像，也称为梯度图像。

梯度常用于检测边缘，在边缘检测会详细介绍。

六、频率域滤波

6.1 傅里叶变换

6.1.1 傅里叶级数

傅里叶级数：任何周期函数都可表示为不同频率的正弦函数和或余弦函数和，其中每个正弦函数和或余弦函数和都有不同的系数。

f(t)=\sum_{n=-\infty}^\infty c_ne^{j\frac {2\pi n} {T}t}

其中，

c_n=\frac 1T\int_{-T/2}^{T/2}f(t)e^{-j\frac {2\pi n} {T}t}dt,n=0,\pm 1,\pm 2,…

是系数。此篇j表示虚数单位： $j^2=-1$ 。

6.1.2 傅里叶变换

傅里叶变换：（曲线下方面积有限的）非周期函数也能用正弦函数和/或余弦函数乘以加权函数的积分来表示

这表明用傅里叶级数或变换表示的函数可由逆过程完全重建（复原），而不丢失信息；允许我们工作在傅里叶域，然后返回到函数的原始域中，而不会丢失任何信息。

计算机慢慢出现了快速傅里叶变换算法（FFT），使用FFT进行频率域处理比不可分离核的空间域处理要快。

6.1.3 冲激函数及其取样（筛选）性质

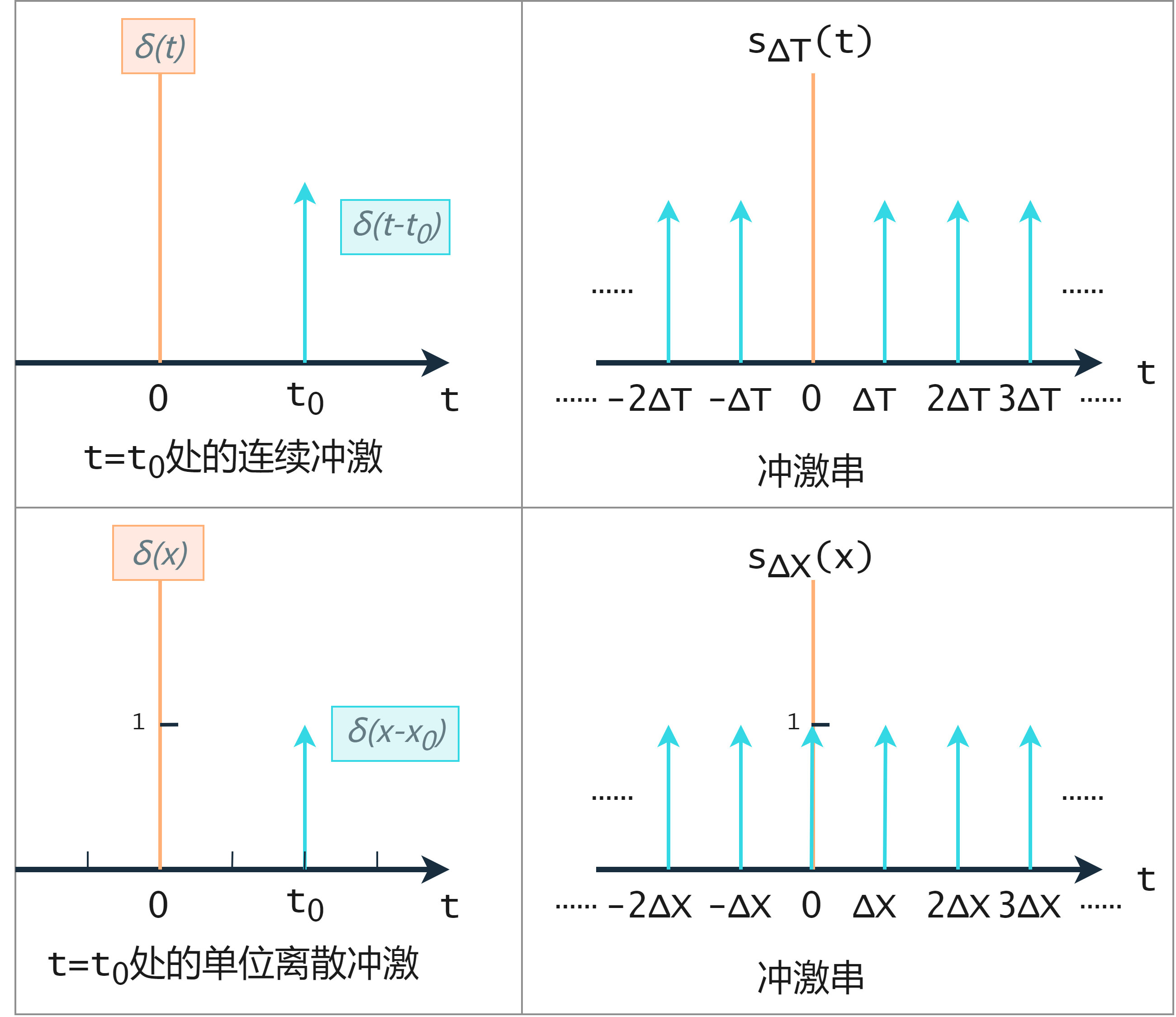
连续变量t在t=0处的单位冲激表示为 $\delta(t)$ ，其定义为：

\delta(t)=\begin{cases} \infty,&t=0\\ 0, &t\neq 0 \end{cases}

该定义被限制满足：

\int_{-\infty}^{\infty}\delta(t)dt=1

当t解释为时间时，冲激可视作幅度为无线、持续时间为0、具有单位面积的尖峰信号。

冲激具有关于积分的所谓 取样性质 ：

\int_{-\infty}^{\infty}f(t)\delta(t)dt=f(0)

对其一般化，任意一点 $t_0$ 的冲激表示为 $\delta(t-t_0)$ ，有：

\int_{-\infty}^{\infty}f(t)\delta(t-t_0)dt=f(t_0)

举一个小例子，取 $f(t)=\cos(t)$ ，则使用冲激 $\delta(t-\pi)$ 得到取样 $f(\pi)=\cos(\pi)=-1$ 。

冲激串则是无穷多个冲激 $\Delta T$ 单位的和：

s_{\Delta T}(t)=\sum_{k=-\infty}^{\infty}\delta(t-k\Delta T)

单位离散冲激 $\delta(x)$ 在离散系统的作用域处理连续变量时冲激 $\delta(t)$ 作用相同，定义为：

\delta(x)=\begin{cases} 1,&x=0\\ 0, &x\neq 0 \end{cases}

该定义被限制的离散等效形式为：

\sum_{x=-\infty}^{\infty}\delta(x) = 1

离散变量的取样性质的形式为：

\sum_{x=-\infty}^{\infty}f(x)\delta(x)=f(0)

一般式为：

\sum_{x=-\infty}^{\infty}f(x)\delta(x-x_0)=f(x_0)

小结：

项	连续变量t	离散变量x
在0处的单位冲激	$\delta(t)=\begin{cases}\infty,&t=0\\0, &t\neq 0\end{cases}$	$\delta(x)=\begin{cases}1,&x=0\\0, &x\neq 0\end{cases}$
单位冲激满足	$\int_{-\infty}^{\infty}\delta(t)dt=1$	$\sum_{x=-\infty}^{\infty}\delta(x) = 1$
取样性质	$\int_{-\infty}^{\infty}f(t)\delta(t)dt=f(0)$	$\sum_{x=-\infty}^{\infty}f(x)\delta(x)=f(0)$
取样性质一般化	$\int_{-\infty}^{\infty}f(t)\delta(t-t_0)dt=f(t_0)$	$\sum_{x=-\infty}^{\infty}f(x)\delta(x-x_0)=f(x_0)$

冲激串：

s_{\Delta T}(t)=\sum_{k=-\infty}^{\infty}\delta(t-k\Delta T)

6.1.4 连续单变量函数的傅里叶变换

连续变量t的连续函数f(t)的傅里叶变换 $\Im\{f(t)\}$ 表示，它定义为：

\Im\{f(t)\}=\int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt

上式中， $\mu$ 为连续变量，积分变量为t，所以 $\Im\{f(t)\}$ 只是 $\mu$ 的函数，即 $\Im\{f(t)\}=F(\mu)$ ，所以 $f(t)$ 的傅里叶变换也可以写为：

F(\mu)=\int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt \quad ①

相反，已知 $F(\mu)$ 是可以通过傅里叶反变换得到 $f(t)$ ，为：

f(t)=\int_{-\infty}^{\infty}F(\mu)e^{j2\pi \mu t}dt\quad ②

称①式和②式共同构成傅里叶变换对，通常表示为 $f(t) \Leftrightarrow F(\mu)$ 。双箭头表明傅里叶正变换得到右侧表达式，而左侧表达式是取右侧表达式的傅里叶反变换得到。

利用欧拉公式 $e^{j\theta}=\cos\theta+j\sin\theta$ ，将式①变成

F(\mu)=\int_{-\infty}^{\infty}f(t)[\cos(2\pi\mu t)-j\sin(2\pi\mu t)]dt

可以看到，如果f(t)为实数，则变换通常是复数。傅里叶变换式f(t)乘以正弦函数的展开式，而其中正弦函数的频率由 $\mu$ 值决定。因此积分后留下的唯一变量是频率，故称傅里叶变换域是频率域。

讨论中， $t$ 可以表示任何连续变量，并且频率变量 $\mu$ 的单位取决于 $t$ 的单位。

举个例子：

对盒式函数进行傅里叶变换，有

F(\mu)=\int_{-\infty}^{\infty}f(t)e^{-j2\pi\mu t}dt=\int_{-W/2}^{W/2}Ae^{-j2\pi\mu t}dt\\ =\frac {-A} {j2\pi\mu}\Big[e^{-j2\pi\mu t}\Big]^{W/2}_{-W/2}=\frac {-A} {j2\pi\mu}\Big[e^{-j\pi\mu W}-e^{j\pi\mu W}\Big]\\ =\frac {A} {j2\pi\mu}\Big[e^{j\pi\mu W}-e^{-j\pi\mu W}\Big]=AW\frac {\sin(\pi\mu W)} {\pi\mu W}

上式用到了 $\sin\theta=(e^{j\theta}-e^{-j\theta})/2j$

傅里叶变换中包含复数项，这是为了显示变换的幅值（一个实量）的一种约定。这个幅值称为傅里叶频谱或频谱：

\vert F(\mu)\vert=AW\vert\frac{\sin(\pi\mu W)} {\pi\mu W}\vert

$F(\mu)$ 与频率的关系曲线如下：

该曲线的关键性质：

$F(\mu)$ 和 $\vert F(\mu)\vert$ 的零值都与盒式函数的宽度W成反比；
到原点的距离越大，旁瓣的高度随到原点的举例增加而减小；
函数向μ的正负方向无限扩展。

再举一个冲激傅里叶变换的例子。

位于原点的单位冲激的傅里叶变换由上面式①得：

\Im \{\delta(t)\}=F(\mu)=\int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt=\int_{\infty}^{\infty}\delta(t)e^{-j2\pi\mu t}dt=e^{-j2\pi\mu_0}=e^0=1

这就是空间域原点位置的一个冲激的傅里叶变换，在频率域中是一个常数。

当 $t=t_0$ 处一个冲击傅里叶变换是：

\Im \{\delta(t)\}=F(\mu)=\int_{\infty}^{\infty}\delta(t-t_0)e^{-j2\pi\mu t}dt=\int_{-\infty}^{\infty}e^{-j2\pi\mu t}\delta(t-t_0)dt=e^{-j2\pi\mu t_0}

上式使用了取样一般化性质。 $e^{-j2\pi\mu t_0}$ 表示中心在复平面原点的一个单位圆。

观察式①式②

F(\mu)=\int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt \\ f(t)=\int_{-\infty}^{\infty}F(\mu)e^{j2\pi \mu t}dt\quad

发现只有指数符号不同。因此如果函数f(t)有傅里叶变换F(μ)，那么求该函数在点t的值F(t)时，一定有变换f(-μ)。利用这种对称性质，将冲激 $\delta(t-t_0)$ 的傅里叶变换 $e^{-j2\pi\mu t_0}$ 得到函数 $e^{-j2\pi\mu t_0}$ 的变换为 $\delta(-\mu-t_0)$ 。令 $-t_0=a$ ，可得 $e^{j2\pi a t}$ 的变换是 $\delta(-\mu+a)=\delta(\mu+a)$

冲激串 $s_{\Delta T}(t)$ 是周期为 $\Delta T$ 的周期函数：

s_{\Delta T}(t)=\sum_{k=-\infty}^{\infty}\delta(t-k\Delta T)

因此可以表示为傅里叶级数：

s_{\Delta T}(t)=\sum_{k=-\infty}^{\infty}c_ne^{j\frac{2\pi n} {\Delta T}t},\\ c_n=\frac{1} {\Delta T}\int_{-\Delta T/2}^{\Delta T/2}S_{\Delta T}(t)e^{-j\frac{2\pi n} {\Delta T}t}dt

由于区间 $\big[-\Delta T/2,\Delta T/2\big]$ 上积分仅包含原点的冲激，故上式简化为：

c_n=\frac{1} {\Delta T}\int_{-\Delta T/2}^{\Delta T/2}\delta(t)e^{-j\frac{2\pi n} {\Delta T}t}dt=\frac{1} {\Delta T}e^0=\frac{1} {\Delta T}

于是傅里叶级数变成：

s_{\Delta T}(t)=\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}e^{j\frac{2\pi n} {\Delta T}t}

由 $\Im \{\delta(t-t_0)\}=e^{-j2\pi\mu t_0}$ ，得到：

\Im \{e^{j\frac{2\pi n} {\Delta T}t}\}=\delta(\mu-\frac{n} {\Delta T})

再由于和的傅里叶变换等于各分量的傅里叶变换之和，所以周期冲激串的傅里叶变换 $S(\mu)$ 是：

\tilde{S}(\mu)=\Im\{s_{\Delta T}(t)\}=\Im\{\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}e^{j\frac{2\pi n} {\Delta T}t}\}=\frac{1} {\Delta T}\Im\{\sum_{n=-\infty}^{\infty}e^{j\frac{2\pi n} {\Delta T}t}\}=\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}\delta(\mu-\frac{n} {\Delta T})

上述结果可得，周期为 $\Delta T$ 的冲激串的傅里叶变换仍然是冲激串，其周期变为 $1/\Delta T$ 。

6.1.5 傅里叶变换与卷积

卷积：空间域中两个函数的卷积的傅里叶变换，等于频率域中两个函数的傅里叶变换的乘积。

设f(t)和h(t)为两个连续函数，F(t)和H(t)为f(t)和h(t)的傅里叶变换，则有：

(f★h)(t)\Leftrightarrow(H\cdot F)(\mu)\\ (f\cdot h)(t)\Leftrightarrow(H★F)(\mu)

6.1.6 取样和取样函数的傅里叶变换

取样：对连续函数转换为一系列的离散值。

\tilde{f}(t)=f(t)s_{\Delta T}(t)=\sum_{n=-\infty}^{\infty}f(t)\delta(t-n\Delta T)

f_k=\int_{-\infty}^{\infty}f(t)\delta(t-k\Delta T)dt=f(k\Delta T)

对取样后的函数 $\tilde{f}(t)$ 的傅里叶变换 $\tilde{F}(\mu)$ 是：

\tilde{F}(\mu)=\Im\{\tilde{f}(t)\}=\Im\{f(t)s_{\Delta T}(t)\}=(F★S)(\mu)

其中， $S(\mu)$ 是冲激串的傅里叶变换：

S(\mu)=\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}\delta(\mu-\frac{n} {\Delta T})

直接得 $F(\mu)$ 和 $S(\mu)$ 的卷积：

\tilde{F}(\mu)=(F★S)(\mu)=\int_{-\infty}^{\infty}F(\tau)S(\mu-\tau)d\tau\\ =\frac{1} {\Delta T}\int_{-\infty}^{\infty}F(\tau)\sum_{n=-\infty}^{\infty}\delta\big(\mu-\tau-\frac{n} {\Delta T}\big)d\tau\\ =\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}F(\tau)\delta\big(\mu-\tau-\frac{n} {\Delta T}\big)d\tau\\ =\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}F(\mu-\frac{n} {\Delta T})

6.1.7 单变量离散傅里叶变换DFT

一维离散傅里叶变换：

F_m=\sum_{n=0}^{M-1}f_ne^{-j2\pi mn/M},m=0,1,2…,M-1

一维离散傅里叶逆变换：

f_n=\frac{1} {M}\sum_{m=0}^{M-1}F_me^{j2\pi mn/M},n=0,1,2…,M-1

6.1.8 二变量离散傅里叶变换

二维离散傅里叶变换：

F(\mu,\nu)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(\mu x/M+\nu y/N)}

二维离散傅里叶逆变换：

f(x,y)=\frac{1} {MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}F(\mu,\nu)e^{j2\pi(\mu x/M+\nu y/N)}

6.1.9 代码

先了解以下函数：

1	int getOptimalDFTSize(int vecsize)

vecsize为向量尺寸大小，该函数用于返回给定向量尺寸经过DFT变换后结果的最优尺寸大小。

1	void copyMakeBorder(InputArray src, OutputArray dst, int top, int bottom, int left, int right, int borderType, const Scalar& value = Scalar())

该函数用于扩充图像边界，参数如下：

src：输入图像；
dst：输出与输入图像相同类型图像；
top、bottom、left、right：在图像的四个方向上扩充像素值；
borderType：边界类型，常见取值为BORDER_CONSTANT；
value：边界类型为BORDER_CONSTANT时表示边界值。

1	void dft(InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0)

该函数为OpenCV提供的傅里叶变换函数，参数如下：

src：输入图像；
dst：输出图像；
flags：转换标识符，默认为0。也有以下取值，DFT_INVERSE（用一维或二维逆变换取代默认的正向变换）、DFT_SCALE（缩放比例标识符，根据数据元素个数平均求出缩放结果）、DFT_ROWS（对输入矩阵的每行进行正向或反向傅里叶变换）、DFT_COMPLEX_OUTPUT（对一维或二维实数数组进行正向变换，结果是复数阵列，是默认）、DFT_REAL_OUTPUT（对一维或二维复数数组进行逆向变换）；
nonzeroRows：当其不为0时函数会假设输入数组（没有设置DFT_INVERSE）的第一行或第一个输出数组（设置了DFT_INVERSE）包含非零值。

1	void magnitude(InputArray x, InputArray y, OutputArray magnitude)

该函数用于计算二维矢量的幅值，参数如下：

x：浮点型数组的x坐标矢量，即实部；
y：浮点型数组的y坐标矢量，必须和x尺寸相同；
magnitude：与x类型和尺寸相同的输出数组；

其计算公式为：

dst(I)=\sqrt{x(I)^2+y(I)^2}

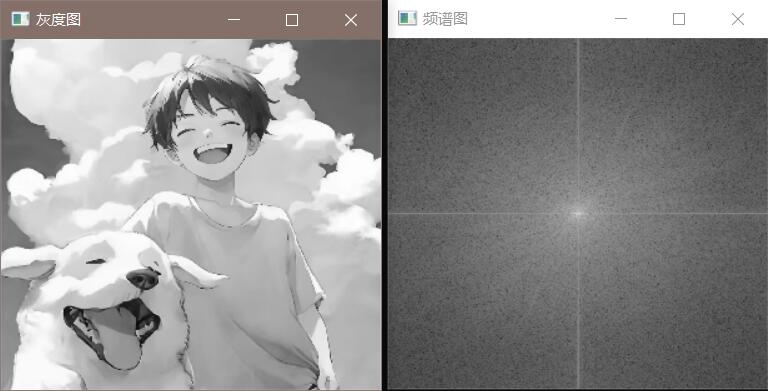
#include <opencv2/opencv.hpp>
#include <iostream>
#include <cmath>

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_img)
{
    // 拓展图像矩阵，为2，3，5的倍数时运算速度快
    int m = cv::getOptimalDFTSize(input.rows);
    int n = cv::getOptimalDFTSize(input.cols);
    cv::copyMakeBorder(input, input, 0, m - input.rows, 0, n - input.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 创建planes存储复数的实部和虚部
    cv::Mat planes[] = { cv::Mat_<float>(input), cv::Mat::zeros(input.size(),CV_32F) };

    // 从多个单通道数组中创建一个多通道数组trf_img。
    // 函数Merge将几个数组合并为一个多通道阵列，即输出数组的每个元素将是输入数组元素的级联
    cv::merge(planes, 2, trf_img);  

    // 进行傅里叶变换
    cv::dft(trf_img, trf_img);

    // 将trf_img拆分到planes数组
    cv::split(trf_img, planes);

    // 计算复数的幅值，即频谱图，保存在output
    cv::magnitude(planes[0], planes[1], output);

    // 赋值计算过大，进行处理
    output += cv::Scalar(1);    //像素加一防止log(0)
    log(output, output);    // 进行对数运算
    cv::normalize(output, output, 0, 1, cv::NORM_MINMAX);   // 归一化

    // 剪切和重分布幅度图像限
    output = output(cv::Rect(0, 0, output.cols & -2, output.rows & -2));

    // 重新排列傅里叶图像中的象限，使原点位于图像中心
    int cx = output.cols / 2;
    int cy = output.rows / 2;
    cv::Mat q0(output, cv::Rect(0, 0, cx, cy));
    cv::Mat q1(output, cv::Rect(cx, 0, cx, cy));
    cv::Mat q2(output, cv::Rect(0, cy, cx, cy));
    cv::Mat q3(output, cv::Rect(cx, cy, cx, cy));

    // 交换象限中心化
    cv::Mat tmp;
    q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);
    q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);

}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg", 0);
    cv::Mat image_output, image_trf;

    cv::namedWindow("灰度图", cv::WINDOW_NORMAL);
    cv::imshow("灰度图", image);

    DFT(image, image_output, image_trf);

    cv::namedWindow("频谱图", cv::WINDOW_NORMAL);
    cv::imshow("频谱图", image_output);

    cv::waitKey(0);
    return 0;
}

效果展示：

6.2 频谱图

频谱图有以下规律：

频谱图从中心点到四周，频率越来越大；
频谱图中心点一般最亮，与原图像平均亮度相关；
频率域滤波就是改变频谱图中高频率或者低频率的值.
频谱图中的点关于中心点对称，对称的两点表示某个频率的波。
两个对称点离中心点的距离代表频率的高低，离中心点越远代表的频率越高。
两个对称点的亮度表示波的幅值，越亮幅值越大。
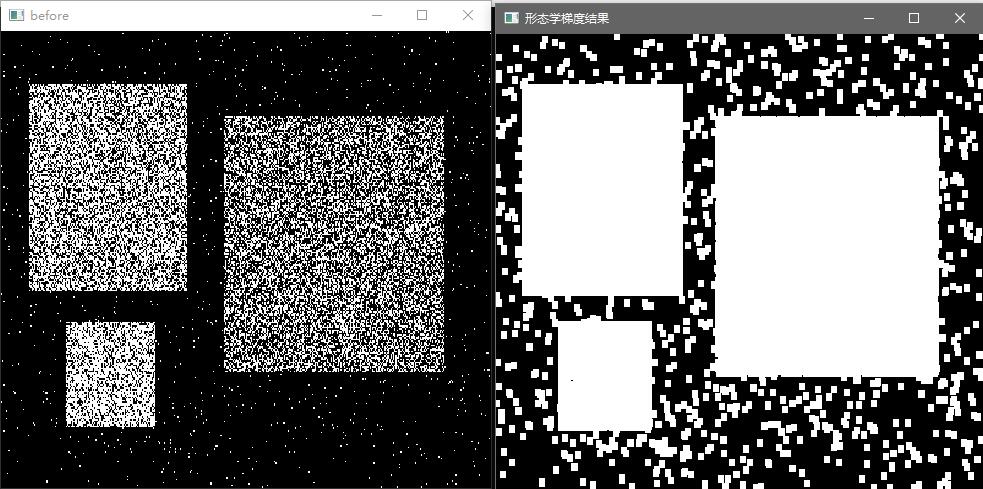
图像中，低频率代表灰度变化缓慢的信息；高频率代表变化剧烈的信息，如边缘及噪声等。在6中，低频区越亮代表变化缓慢的区域较多，高频区越亮代表图像细节很多。
对称点所在直线的方向为波的方向，与原图中对应的线性信息垂直。如下图，图中有一组平行的线，在频谱图垂直方向也有一条较亮的线（可用于方向滤波，增强或者滤除某个方向的线性特征）。

6.3 低通滤波

6.3.1 理想低通滤波

通过设置频率半径，半径内的频率大小不变，半径外的频率置为0，保留了低频区，滤除了高频区。

传递函数为：

H(u,v)= \begin{cases} 1,\quad D(u,v)\leq D_0\\ 0, \quad D(u,v)>D_0 \end{cases}

其中， $D_0$ 是一个正常数， $D(u,v)$ 是频率域中点(u,v)到P×Q频率矩形中心的距离， $D(u,v)=[(u-P/2)^2+(v-Q/2)^2]^{1/2}$ 。

理想低通滤波器由于进行傅里叶变换和傅里叶逆变换时的差异，会导致振铃效应，一般很少使用。

振铃效应：指输出图像的灰度剧烈变化处产生的震荡，就好像钟被敲击后产生的空气震荡

代码：

// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"
#include "Salt.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    Salt(image, 100000);    // 添加100k个噪点

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 理想低通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
            if ((i - cx) * (i - cx) + (j - cy) * (j - cy) > r * r)
            {
                trf_real.at<float>(i, j) = 0;
                trf_imag.at<float>(i, j) = 0;
            }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

为了更好的效果，手动添加噪声：

// Salt.h
#pragma once
#include <opencv2/opencv.hpp>
#include <random>

void Salt(cv::Mat input, int n);

// 噪声文件Salt.cpp
#include "Salt.h"

void Salt(cv::Mat input, int n)
{
    std::default_random_engine generator;
    std::uniform_int_distribution<int>row(0, input.rows - 1);
    std::uniform_int_distribution<int>col(0, input.cols - 1);
    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = row(generator);
        j = col(generator);
        if (input.channels() == 1)
            input.at<uchar>(i, j) = 255;
        else if (input.channels() == 3)
            input.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 255, 255);
    }
}

对图像傅里叶变换：

// DFT.h
#pragma once
#include <opencv2/opencv.hpp>
#include <cmath>

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr);

// DFT.cpp
#include "DFT.h"

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr)
{
    // 扩展图像，优化速度
    int n = cv::getOptimalDFTSize(input.rows);
    int m = cv::getOptimalDFTSize(input.cols);
    cv::copyMakeBorder(input, input, 0, n - input.rows, 0, m - input.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 用于存储傅里叶变换的实部和虚部
    cv::Mat planes[] = { cv::Mat_<float>(input), cv::Mat::zeros(input.size(), CV_32F) };

    cv::merge(planes, 2, trf_arr);

    cv::dft(trf_arr, trf_arr);

    cv::split(trf_arr, planes);
    cv::Mat trf_img_real = planes[0];
    cv::Mat trf_img_imag = planes[1];

    // 计算复数的幅值，保存在output中
    cv::magnitude(planes[0], planes[1], output);

    // 优化幅值大小
    output += cv::Scalar(1);
    log(output, output);
    cv::normalize(output, output, 0, 1, cv::NORM_MINMAX);

    output = output(cv::Rect(0, 0, output.cols & -2, output.rows & -2));

    int cx = output.cols / 2, cy = output.rows / 2;
    cv::Mat q0(output, cv::Rect(0, 0, cx, cy)), q1(output, cv::Rect(cx, 0, cx, cy));
    cv::Mat q2(output, cv::Rect(0, cy, cx, cy)), q3(output, cv::Rect(cx, cy, cx, cy));
    cv::Mat tmp;

    // 交换区域使得原点位于中心
    q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);
    q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);

    // 复数的实数部分交换
    cv::Mat q00(trf_img_real, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q01(trf_img_real, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q02(trf_img_real, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q03(trf_img_real, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q00.copyTo(tmp); q03.copyTo(q00); tmp.copyTo(q03);        //左上与右下进行交换
    q01.copyTo(tmp); q02.copyTo(q01); tmp.copyTo(q02);        //右上与左下进行交换

    // 复数的虚数部分交换
    cv::Mat q10(trf_img_imag, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q11(trf_img_imag, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q12(trf_img_imag, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q13(trf_img_imag, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q10.copyTo(tmp); q13.copyTo(q10); tmp.copyTo(q13);        //左上与右下进行交换
    q11.copyTo(tmp); q12.copyTo(q11); tmp.copyTo(q12);        //右上与左下进行交换

    planes[0] = trf_img_real;
    planes[1] = trf_img_imag;
    cv::merge(planes, 2, trf_arr);    // 将傅里叶变换的复数结果保存在trf_arr
}

效果展示：

6.3.2 高斯低通滤波

高斯低通滤波器的传递函数为：

H(u,v)=e^{-D^2(u,v)/2\sigma^2}

其中， $D(u,v)$ 是P×Q频率矩形中心到矩形中包含的任意一点(u,v)的距离，令 $\sigma=D_0$ ，

H(u,v)=e^{-D^2(u,v)/2D_0^2}

那么 $D_0$ 是截止频率（设置半径）。当 $D(u,v)=D_0$ 时，高斯低通滤波器传递函数下降到其最大值1.0的0.607。

由于高斯函数的傅里叶变换还是高斯函数，所以高斯低通滤波器没有振铃效应。

代码：

DFT.h、DFT.cpp、Salt.h、Salt.cpp同上。

// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"
#include "Salt.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    Salt(image, 100000);    // 添加100k个噪点

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 高斯低通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 80;    // 滤波半径
    float h;

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            h = exp(-((i - cx) * (i - cx) + (j - cy) * (j - cy)) / (2.0 * r * r));
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

6.3.4 巴特沃斯低通滤波

巴特沃斯低通滤波器的传递函数为：

H(u,v)=\frac {1} {1+[D(u,v)/D_0]^{2n} }

其中， $D(u,v)$ 是P×Q频率矩形中心到矩形中包含的任意一点(u,v)的距离， $D_0$ 是截止频率（设置半径）， $n$ 是巴特沃斯滤波器的阶数。

1阶巴特沃斯滤波器既没有振铃效应也没有负值；2阶巴特沃斯滤波器有轻微振铃效应和较小的负值，但比理想低通滤波器好；高阶巴特沃斯滤波器具有非常明显的振铃效应。2阶和3阶的巴特沃斯滤波器较为合适。

代码：

DFT.h、DFT.cpp、Salt.h、Salt.cpp同上。

// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"
#include "Salt.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    Salt(image, 100000);    // 添加100k个噪点

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 巴特沃斯低通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径
    float h;
    float n = 3;    // 巴特沃斯滤波器阶数
    float d;        // 任意点到中心的距离

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = 1.0 / (1 + pow((d / (r * r)), 2 * n));
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

6.4 高通滤波

6.4.1 理想高通滤波

通过设置频率半径，半径外的频率大小不变，半径内的频率置为0，保留了高频区，滤除了低频区。

而边缘和其他灰度的急剧变化与高频分量有关，故高通滤波器可以实现边缘锐化。

传递函数为：

H(u,v)= \begin{cases} 0,\quad D(u,v)\leq D_0\\ 1, \quad D(u,v)>D_0 \end{cases}

其中， $D_0$ 是一个正常数， $D(u,v)$ 是频率域中点(u,v)到P×Q频率矩形中心的距离， $D(u,v)=[(u-P/2)^2+(v-Q/2)^2]^{1/2}$ 。

代码（DFT代码文件见最后）：

// main.cpp
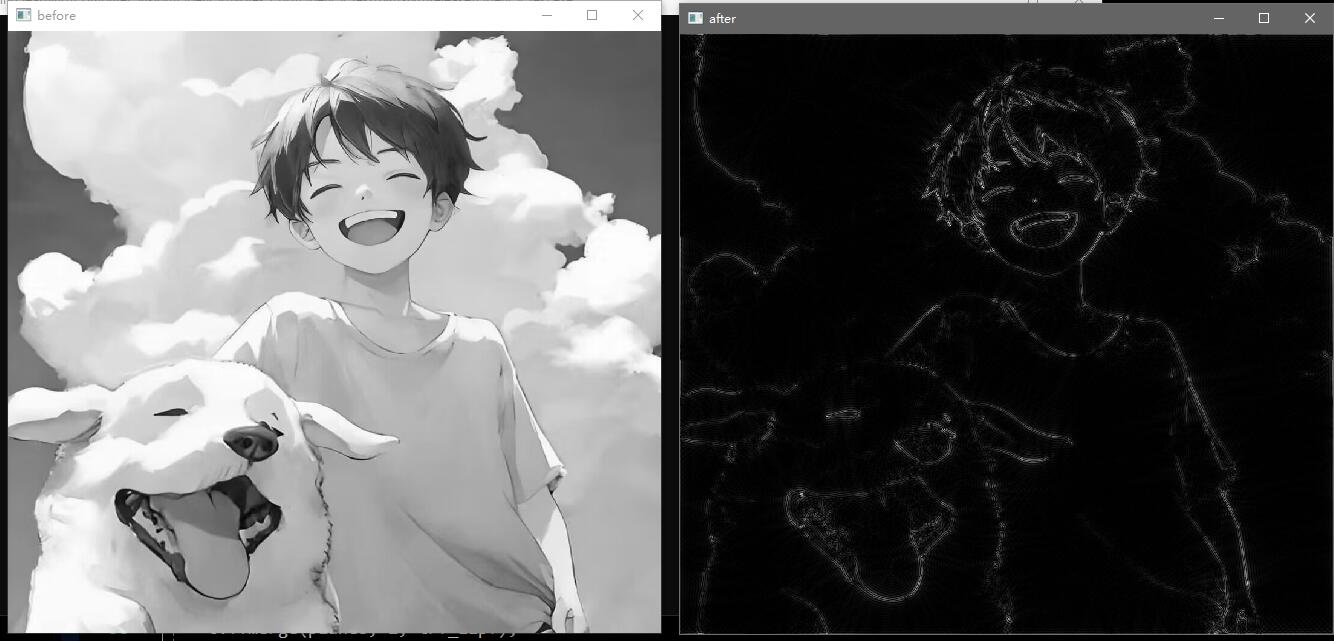
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 理想高通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
            if ((i - cx) * (i - cx) + (j - cy) * (j - cy) < r * r)
            {
                trf_real.at<float>(i, j) = 0;
                trf_imag.at<float>(i, j) = 0;
            }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

6.4.2 高斯高通滤波

高斯低通滤波器的传递函数为：

H_{LP}(u,v)=e^{-D^2(u,v)/2\sigma^2}

则高斯高通滤波器传递函数为：

H_{HP}=1-H_{LP}(u,v)=1-e^{-D^2(u,v)/2D_0^2}

其中， $D(u,v)$ 为中心点到任一点的距离， $D_0$ 为设置半径。

代码（DFT代码文件见最后）：

// main.cpp
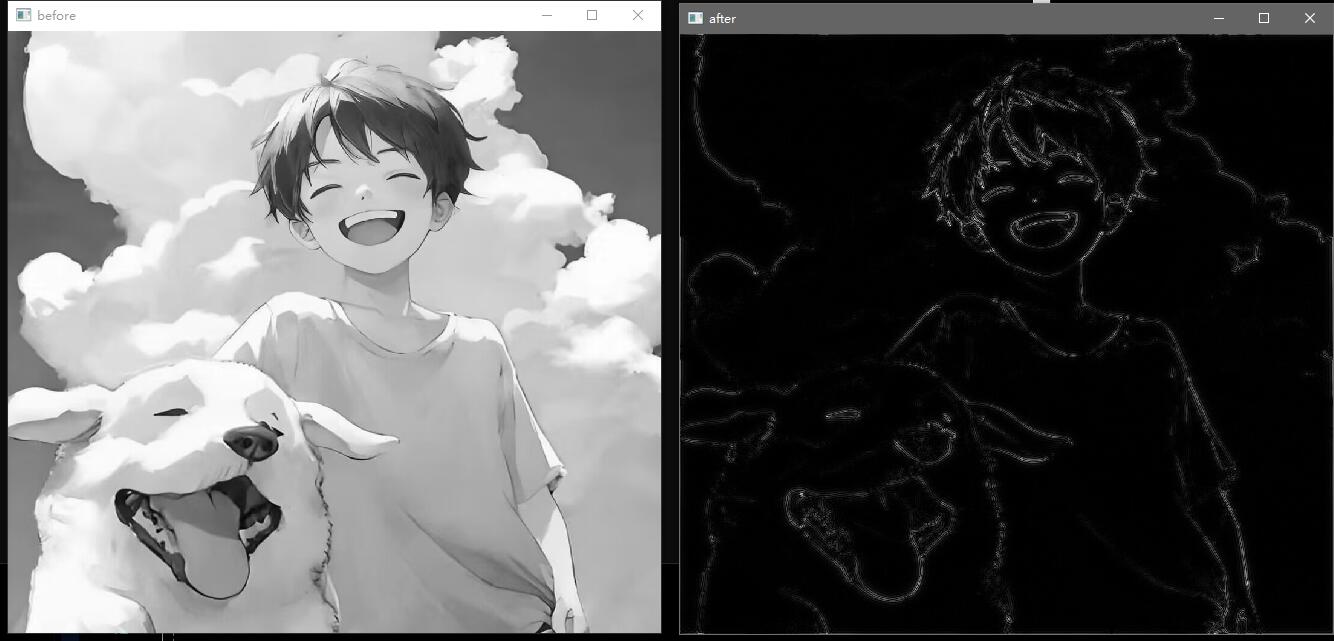
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 高斯高通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径
    float h, d;        // h 为计算量，d 为到中心点的距离

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = 1 - exp(-d / (2.0 * r * r));
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

6.4.3 巴特沃斯高通滤波

巴特沃斯高铁滤波器的传递函数为：

H(u,v)=\frac {1} {1+[D_0/D(u,v)]^{2n} }

其中， $D(u,v)$ 是P×Q频率矩形中心到矩形中包含的任意一点(u,v)的距离， $D_0$ 是截止频率（设置半径）， $n$ 是巴特沃斯滤波器的阶数。

代码（DFT代码文件见最后）：

// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 巴特沃斯高通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径
    float h, d;        // h 为计算量，d为到中心点的距离
    float n = 3;    // 巴特沃斯滤波器阶数

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = 1.0 / (1 + pow(((r * r) / d), 2 * n));
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

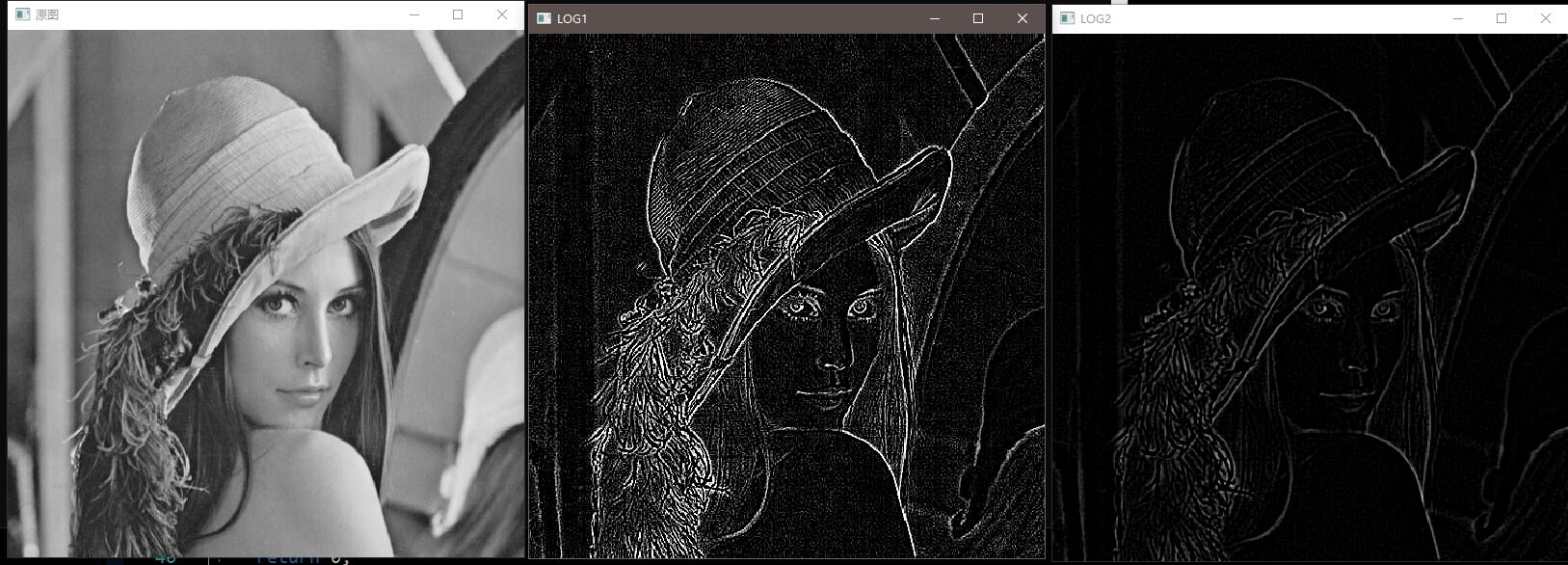
6.4.4 拉普拉斯滤波

频率域中拉普拉斯滤波传递函数为：

H(u,v)=-4\pi^2(u^2+v^2)=-4\pi^2[(u-P/2)^2+(v-Q/2)^2]=-4\pi^2D^2(u,v)

其中， $D(u,v)$ 为中心点到任一点的距离。

具体增强实现：

g(x,y)=f(x,y)+c\nabla^2f(x,y),\nabla^2f(x,y)=\Im^{-1}[H(u,v)F(u,v)]

其中， $F(u,v)$ 是 $f(x,y)$ 的傅里叶变换。

代码：

// main.cpp
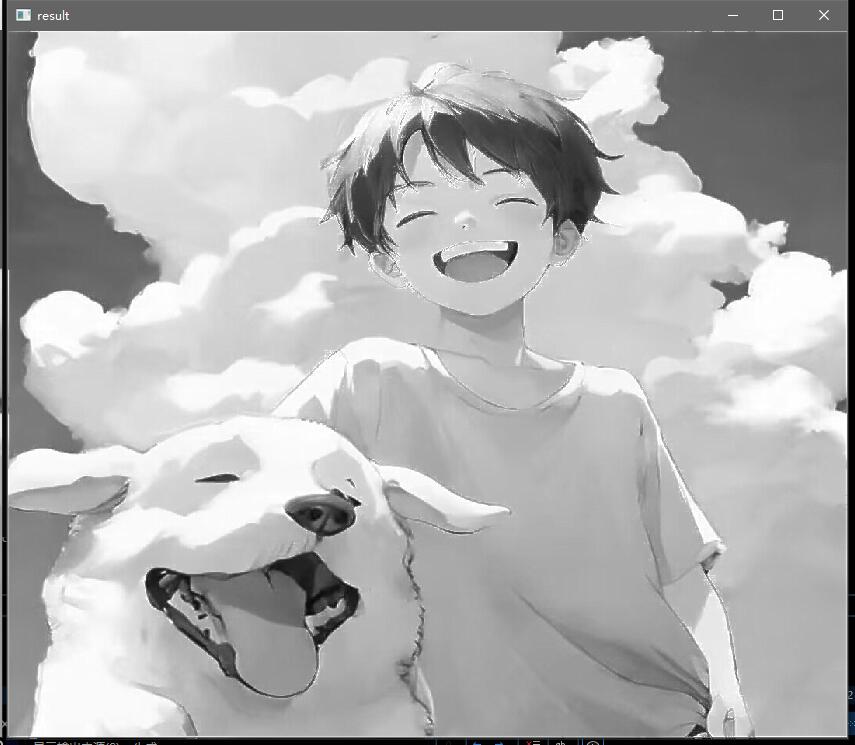
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    /*————————————————————————————拉普拉斯滤波————————————————————————————*/
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    float h, d;        // h 为计算量，d为到中心点的距离
    float pi = 3.1415926;

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = -4 * pi * pi * d;
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);

    /*————————————————————————————标记，实现g(x,y)————————————————————————————*/
    iDft[0].convertTo(iDft[0], CV_8U, 255 / 1.0, 0);
    cv::Mat result(iDft[0].size(), CV_8U);
    for (int i = 0; i < iDft[0].rows; i ++)
        for (int j = 0; j < iDft[0].cols; j ++)
            result.at<uchar>(i, j) = cv::saturate_cast<uchar>(image.at<uchar>(i, j) + iDft[0].at<uchar>(i, j));

    cv::namedWindow("result", cv::WINDOW_NORMAL);
    cv::imshow("result", result);
    cv::waitKey(0);

    return 0;
}

效果展示：

6.4.5 高频强调滤波器

还可以设置可调参数，进行调整影响。高频强调滤波的通用公式是：

g(x,y)=\Im^{-1}\bigg\{\big[k_1+k_2H_{HP}\big]F(u,v)\bigg\}

其中， $k_1\geq0$ 偏移传递函数的值，以便使直流项不为零， $k_2>0$ 控制高频的贡献， $H_{HP}$ 为高通滤波器传递函数， $F(u,v)$ 为图像 $f(u,v)$ 的傅里叶变换。

部分代码示例：

for (int i = 0; i < trf_real.rows; i ++)
    for (int j = 0; j < trf_real.cols; j ++)
    {
        d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
        // 高斯高频强调滤波器
        h = 0.5 + 0.75 * (1 - exp(-d / (2.0 * r * r)));
        trf_real.at<float>(i, j) *= h;
        trf_imag.at<float>(i, j) *= h;
    }

附DFT代码

// DFT.h
#pragma once
#include <opencv2/opencv.hpp>
#include <cmath>

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr);

// DFT.cpp
#include "DFT.h"

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr)
{
    // 扩展图像，优化速度
    int n = cv::getOptimalDFTSize(input.rows);
    int m = cv::getOptimalDFTSize(input.cols);
    cv::copyMakeBorder(input, input, 0, n - input.rows, 0, m - input.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 用于存储傅里叶变换的实部和虚部
    cv::Mat planes[] = { cv::Mat_<float>(input), cv::Mat::zeros(input.size(), CV_32F) };

    cv::merge(planes, 2, trf_arr);

    cv::dft(trf_arr, trf_arr);

    cv::split(trf_arr, planes);
    cv::Mat trf_img_real = planes[0];
    cv::Mat trf_img_imag = planes[1];

    // 计算复数的幅值，保存在output中
    cv::magnitude(planes[0], planes[1], output);

    // 优化幅值大小
    output += cv::Scalar(1);
    log(output, output);
    cv::normalize(output, output, 0, 1, cv::NORM_MINMAX);

    output = output(cv::Rect(0, 0, output.cols & -2, output.rows & -2));

    int cx = output.cols / 2, cy = output.rows / 2;
    cv::Mat q0(output, cv::Rect(0, 0, cx, cy)), q1(output, cv::Rect(cx, 0, cx, cy));
    cv::Mat q2(output, cv::Rect(0, cy, cx, cy)), q3(output, cv::Rect(cx, cy, cx, cy));
    cv::Mat tmp;

    // 交换区域使得原点位于中心
    q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);
    q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);

    // 复数的实数部分交换
    cv::Mat q00(trf_img_real, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q01(trf_img_real, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q02(trf_img_real, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q03(trf_img_real, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q00.copyTo(tmp); q03.copyTo(q00); tmp.copyTo(q03);        //左上与右下进行交换
    q01.copyTo(tmp); q02.copyTo(q01); tmp.copyTo(q02);        //右上与左下进行交换

    // 复数的虚数部分交换
    cv::Mat q10(trf_img_imag, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q11(trf_img_imag, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q12(trf_img_imag, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q13(trf_img_imag, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q10.copyTo(tmp); q13.copyTo(q10); tmp.copyTo(q13);        //左上与右下进行交换
    q11.copyTo(tmp); q12.copyTo(q11); tmp.copyTo(q12);        //右上与左下进行交换

    planes[0] = trf_img_real;
    planes[1] = trf_img_imag;
    cv::merge(planes, 2, trf_arr);    // 将傅里叶变换的复数结果保存在trf_arr
}

6.5 同态滤波

通过一个滤波器传递函数H(u,v)，使用不同可控方法影响低频分量和高频分量。

6.5.1 基本原理

图像f(x,y)可以表示为其照射分量i(x,y)和反射分量r(x,y)的乘积。

图像中，认为低频分量与照射分量相联系，高频分量与反射分量相联系。

f(x,y)=i(x,y)r(x,y)

乘积的傅里叶变换不是傅里叶变换的乘积。

\Im [f(x,y)] \neq \Im[i(x,y)]\Im[r(x,y)]

故令 $z(x,y)=\ln f(x,y)=\ln i(x,y)+\ln r(x,y)$ ，有

\Im[z(x,y)]=\Im[\ln f(x,y)]=\Im[\ln i(x,y)]+\Im[\ln r(x,y)]

Z(u,v)=F_i(u,v)+F_r(u,v)

其中， $F_i(u,v)$ 和 $F_r(x,y)$ 分别是 $\ln i(x,y)$ 和 $\ln r(x,y)$ 的傅里叶变换。

使用滤波器传递函数 $H(u,v)$ 对 $Z(u,v)$ 滤波，有

S(u,v)=H(u,v)Z(u,v)=H(u,v)F_i(u,v)+H(u,v)F_r(u,v)

空间域中滤波后的图像是

s(x,y)=\Im^{-1}[S(u,v)]=\Im^{-1}[H(u,v)F_i(u,v)]+\Im^{-1}[H(u,v)F_r(u,v)]

最后通过取滤波后的结果的指数形成输出图像

g(x,y)=e^{s(x,y)}=e^{\Im^{-1}[H(u,v)F_i(u,v)]}e^{\Im^{-1}[H(u,v)F_r(u,v)]}

记

i_0(x,y)=e^{i'(x,y)}=e^{\Im^{-1}[H(u,v)F_i(u,v)]}

为输出图像的照射分量，

记

r_0(x,y)=e^{r'(x,y)}=e^{\Im^{-1}[H(u,v)F_r(u,v)]}

为输出图像的反射分量。

上述滤波方法过程如下图：

6.5.2 以高斯高通滤波器举例

一般高斯高通滤波器函数：

H(u,v)=1-e^{-D^2(u,v)/2D^2_0}

使用稍微变化的GHPF（Gaussian high-pass filter）：

H(u,v)=(\gamma_H-\gamma_L)\big[1-e^{-cD^2(u,v)/D_0^2}\big]+\gamma_L

其中， $D(u,v)$ 为中心点到任一点的距离， $D_0$ 为设置半径， $\gamma_L$ 和 $\gamma_H$ 为规定频率范围，常数c控制函数的偏斜度，类似于高频强调函数。

变化后的GHPF图像如下：

明显地，减少了低频分量的影响，增加了高频分量的影响。

代码：

// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    /* ——————————对数变换—————————— */
    cv::Mat image_(image.size(), CV_32F);
    for (int i = 0; i < image.rows; i ++)
        for (int j = 0; j < image.cols; j ++)
            image_.at<float>(i, j) = log(image.at<uchar>(i, j) + 0.1);

    DFT(image_, output, trf);    // 对图像进行傅里叶变换

    /* ——————————滤波—————————— */
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 10;    // 滤波半径
    float h, d;        // h 为计算量，d 为到中心点的距离
    float rh = 3, rl = 0.5, c = 5;    // 高频点、低频点、c值

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = (rh - rl) * (1 - exp(-c * d / (r * r))) + rl;
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    /* ——————————指数恢复数值并归一化—————————— */
    cv::exp(iDft[0], iDft[0]);
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    iDft[0].convertTo(iDft[0], CV_8U, 255 / 1.0, 0);
    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

// DFT.h
#pragma once
#include <opencv2/opencv.hpp>
#include <cmath>

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr);

// DFT.cpp
#include "DFT.h"

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr)
{
    // 扩展图像，优化速度
    int n = cv::getOptimalDFTSize(input.rows);
    int m = cv::getOptimalDFTSize(input.cols);
    cv::copyMakeBorder(input, input, 0, n - input.rows, 0, m - input.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 用于存储傅里叶变换的实部和虚部
    cv::Mat planes[] = { cv::Mat_<float>(input), cv::Mat::zeros(input.size(), CV_32F) };

    cv::merge(planes, 2, trf_arr);

    cv::dft(trf_arr, trf_arr);

    cv::split(trf_arr, planes);
    cv::Mat trf_img_real = planes[0];
    cv::Mat trf_img_imag = planes[1];

    // 计算复数的幅值，保存在output中
    cv::magnitude(planes[0], planes[1], output);

    // 优化幅值大小
    output += cv::Scalar(1);
    log(output, output);
    cv::normalize(output, output, 0, 1, cv::NORM_MINMAX);

    output = output(cv::Rect(0, 0, output.cols & -2, output.rows & -2));

    int cx = output.cols / 2, cy = output.rows / 2;
    cv::Mat q0(output, cv::Rect(0, 0, cx, cy)), q1(output, cv::Rect(cx, 0, cx, cy));
    cv::Mat q2(output, cv::Rect(0, cy, cx, cy)), q3(output, cv::Rect(cx, cy, cx, cy));
    cv::Mat tmp;

    // 交换区域使得原点位于中心
    q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);
    q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);

    // 复数的实数部分交换
    cv::Mat q00(trf_img_real, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q01(trf_img_real, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q02(trf_img_real, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q03(trf_img_real, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q00.copyTo(tmp); q03.copyTo(q00); tmp.copyTo(q03);        //左上与右下进行交换
    q01.copyTo(tmp); q02.copyTo(q01); tmp.copyTo(q02);        //右上与左下进行交换

    // 复数的虚数部分交换
    cv::Mat q10(trf_img_imag, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q11(trf_img_imag, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q12(trf_img_imag, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q13(trf_img_imag, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q10.copyTo(tmp); q13.copyTo(q10); tmp.copyTo(q13);        //左上与右下进行交换
    q11.copyTo(tmp); q12.copyTo(q11); tmp.copyTo(q12);        //右上与左下进行交换

    planes[0] = trf_img_real;
    planes[1] = trf_img_imag;
    cv::merge(planes, 2, trf_arr);    // 将傅里叶变换的复数结果保存在trf_arr
}

七、噪声模型及估计和滤波方法

噪声分量的灰度值可视为随机变量，故讨论概率密度函数。

7.1 噪声模型

7.1.1 高斯噪声

概率密度函数（PDF，Probability Density Function）：

p(z)=\frac {1} {\sqrt{2\pi}\sigma}e^{-(z-\overline{z})^2/2\sigma^2},-\infty<z<\infty

其中， $z$ 表示灰度， $\overline{z}$ 表示 $z$ 的均值， $\sigma$ 是 $z$ 的标准差。

7.1.2 瑞利噪声

PDF为：

p(z)=\begin{cases} \frac{2} {b}(z-a)e^{-(z-a)^2/b}&,z\geq a\\ 0&,z<a \end{cases}

当z由瑞利PDF表征时，均值为 $\overline{z}=a+\sqrt{\pi b/4}$ ，方差为 $\sigma^2=\frac{b(4-\pi)} {4}$ 。

7.1.3 爱尔兰（伽马）噪声

PDF为：

p(z)=\begin{cases} \frac{a^bz^{b-1} } {(b-1)!}e^{-az}&,z\geq 0\\ 0&,z<0 \end{cases}

其中，a>b，z的均值为 $\overline{z}=\frac{a} {b}$ ，方差为 $\sigma^2=\frac{b} {a^2}$

7.1.4 指数噪声

PDF为：

p(z)=\begin{cases} ae^{-az}&,z\geq 0\\ 0&,z<0 \end{cases}

其中，a>0，z的均值为 $\overline{z}=\frac{1} {a}$ ，方差为 $\sigma^2=\frac{1} {a^2}$ 。其为爱尔兰PDF在b=1时的特殊情况。

7.1.5 均匀噪声

PDF为：

p(z)=\begin{cases} \frac{1} {b-a}&,a\leq z\leq b\\ 0&,其他 \end{cases}

其中，z的均值为 $\overline{z}=\frac{a+b} {2}$ ，方差为 $\sigma^2=\frac{(b-a)^2} {12}$

7.1.6 椒盐噪声

PDF为：

p(z)=\begin{cases} P_s&,z=2^k-1\\ P_p&,z=0\\ 1-(P_s+P_p)&,z=V \end{cases}

其中，V是区间 $0<V<2^k-1$ 内的任意整数，k是数字图像中灰度值的比特数。像素被盐粒或胡椒噪声污染的概率P为 $P=P_s+P_p$ 。P为噪声密度。

椒盐噪声的均值为 $\overline{z}=(0)P_p+K(1-P_s-P_p)+(2^k-1)P_s$ ，

方差为 $\sigma^2=(0-\overline{z})^2P_p+(K-\overline{z})^2(1-P_s-P_p)+(2^k-1)P_s$ 。

7.2 判别噪声类别

椒盐噪声可以肉眼区分。

其他噪声需要取图像中灰度较为平滑的区域，使用灰度分布图判断。

由上图可知，选取较为平滑的区域，高斯噪声后的直方图与高斯噪声PDF类似，而均匀噪声后的直方图与均匀噪声PDF类似。

上图代码实现

有关函数：

1	void fill(InputOutputArray mat, int distType, InputArray a, InputArray b, bool saturateRange = false);

该函数属于OpenCV 4的RNG类，是一个非静态成员函数，因此在使用的时候不能像使用正常函数一样的直接使用，而需要首先创建一个RNG类的变量，之后通过访问这个变量中函数进行调用这个函数。

该函数参数如下：

mat：用于存放随机数的矩阵，目前只支持低于5通道的矩阵。
distType：随机数分布形式选择标志，目前生成的随机数支持均匀分布（RNG::UNIFORM，0）和高斯分布（RNG::NORMAL，1）。
a：确定分布规律的参数。当选择均匀分布时，该参数表示均匀分布的最小下限；当选择高斯分布时，该参数表示高斯分布的均值。
b：确定分布规律的参数。当选择均匀分布时，该参数表示均匀分布的最大上限；当选择高斯分布时，该参数表示高斯分布的标准差。
saturateRange：预饱和标志，仅用于均匀分布。

#include <iostream>
#include <opencv2/opencv.hpp>

// 添加高斯噪声
void GaussianNoise(cv::Mat input, cv::Mat &output)
{
    cv::RNG rng;
    cv::Mat noice = input.clone();
    output = input.clone();
    rng.fill(noice, cv::RNG::NORMAL, 10, 50);    // 使用NORMAL参数添加高斯噪声
    output = input + noice;
}

// 添加均匀噪声
void UniformNoise(cv::Mat input, cv::Mat &output)
{
    cv::RNG rng;
    cv::Mat noice = input.clone();
    output = input.clone();
    rng.fill(noice, cv::RNG::UNIFORM, 10, 50);    // 使用UNIFORM参数添加高斯噪声
    output = input + noice;
}

void getHist(cv::Mat& input, cv::Mat& histImage)
{
    // 划出感兴趣区域
    cv::Mat ioa(cv::Mat::zeros(input.size(), CV_8U));
    for (int i = 0; i < 100; i ++)
        for (int j = 900; j < 1000; j ++)
            ioa.at<uchar>(i, j) = 255;
    // 框出感兴趣区域
    cv::rectangle(input, cv::Rect(900, 0, 100, 100), cv::Scalar(0, 0, 255), 5);

    /* ————————计算并绘制直方图———————— */
    cv::Mat hist;
    int hsize = 256;    // 直方图区间数
    float ranges[] = { 0, 256 };   // 统计像素值的区间
    const float *hRanges = { ranges };
    // 计算直方图的输出值
    cv::calcHist(&input, 1, 0, ioa, hist, 1, &hsize, &hRanges, true, false);

    int hist_h = 300, hist_w = 512; // 直方图图像高和宽
    int bin_w = hist_w / hsize; // 区间

    // 直方图图像
    histImage = cv::Mat(hist_h, hist_w, CV_8UC3, cv::Scalar(255, 255, 255));
    // 直方图输出值归一化到0~255
    cv::normalize(hist, hist, 0, hist_h, cv::NORM_MINMAX, -1, cv::Mat());

    for (int i = 1; i < hsize; i ++)
        cv::line(histImage, cv::Point((i - 1) * bin_w, hist_h - cvRound(hist.at<float>(i - 1))), cv::Point((i) *bin_w, hist_h - cvRound(hist.at<float>(i))), cv::Scalar(100, 100, 100), 2);
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2, hi1, hi2, hi;

    GaussianNoise(input, output1);
    UniformNoise(input, output2);
    getHist(input, hi);
    getHist(output1, hi1);
    getHist(output2, hi2);

    cv::namedWindow("原图", cv::WINDOW_NORMAL);
    cv::imshow("原图", input);
    cv::namedWindow("原图直方图", cv::WINDOW_NORMAL);
    cv::imshow("原图直方图", hi);
    cv::namedWindow("高斯噪声后图", cv::WINDOW_NORMAL);
    cv::imshow("高斯噪声后图", output1);
    cv::namedWindow("均匀噪声后图", cv::WINDOW_NORMAL);
    cv::imshow("均匀噪声后图", output2);
    cv::namedWindow("高斯噪声后直方图", cv::WINDOW_NORMAL);
    cv::imshow("高斯噪声后直方图", hi1);
    cv::namedWindow("均匀噪声后直方图", cv::WINDOW_NORMAL);
    cv::imshow("均匀噪声后直方图", hi2);

    cv::waitKey(0);

    return 0;
}

7.3 常见的空间滤波方法

7.3.1 均值滤波器

算术均值滤波器：也是盒式滤波器，平滑图像中的局部变化，会降低噪声，也会模糊图像。
几何均值滤波器：比算术均值滤波器相比丢失细节少。
谐波平均滤波器：适合处理高斯噪声及盐粒噪声，但不能处理胡椒噪声。
逆谐波均值滤波器：调节阶数有不同的效果。

7.3.2 统计排序滤波器

中值滤波器：处理单极、双极冲激噪声更好，也能有效降低某些随机噪声，丢失细节更少。
最大最小值滤波器：分别减少暗点和亮点，如胡椒噪声和盐粒噪声。可通过最大值滤波器削减胡椒噪声，通过最小值滤波器削减盐粒噪声。
中点滤波器：适合处理随机分布的噪声，如高斯噪声和均匀噪声。
修正阿尔法均值滤波器：适合处理多种混合噪声，如高斯噪声和椒盐噪声。

7.3.3 自适应滤波器

自适应局部降噪滤波器：与均值滤波器比结果更清晰。
自适应中值滤波器：平滑时保留图像细节。

八、滤波器

8.1 均值滤波器

8.1.1 算术平均滤波器

算术均值滤波器：也是盒式滤波器，平滑图像中的局部变化，会降低噪声，也会模糊图像。表达式如下，其中 $\hat f$ 为复原的图像， $S_{xy}$ 表示中心为(x,y)、大小为m×n的矩形子图像窗口的一组坐标， $g(x,y)$ 为被污染的图像：

\hat f(x,y)=\frac{1} {mn}\sum_{(r,c)\in S_{xy} }g(r,c)

代码（Salt的相关代码见最后）：

8.1.2 几何均值滤波器

几何均值滤波器：比算术均值滤波器相比丢失细节少。表达式如下，其中 $\hat f$ 为复原的图像， $S_{xy}$ 表示中心为(x,y)、大小为m×n的矩形子图像窗口的一组坐标， $g(x,y)$ 为被污染的图像：

\hat f(x,y)=\bigg[\prod_{(r,c)\in S_{xy} }g(r,c)\bigg]^{\frac {1} {mn} }

代码（Salt的相关代码见最后）：

#include <iostream>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void GeometricMeanFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    // 以镜像复制扩充边界
    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    double k = m * n;
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            double sum = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                    sum += log10(input.at<uchar>(i + x, j + y) + 0.1);
            // 使用对数进行运算指数，避免数值过大
            sum /= k;
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = round(pow(10, sum));
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现方法
    GeometricMeanFilter(input, output1, 7, 7);
    // OpenCV盒式滤波器
    cv::blur(input, output2, cv::Size(7, 7));

    cv::namedWindow("几何均值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("几何均值滤波器", output1);
    cv::namedWindow("算术均值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("算术均值滤波器", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

8.1.3 谐波均值滤波器

谐波平均滤波器：适合处理高斯噪声及盐粒噪声，但不能处理胡椒噪声。表达式如下，其中 $\hat f$ 为复原的图像， $S_{xy}$ 表示中心为(x,y)、大小为m×n的矩形子图像窗口的一组坐标， $g(x,y)$ 为被污染的图像：

\hat f(x,y)=\frac{mn} {\sum_{(r,c)\in S_{xy} }\frac{1} {g(r,c)} }

代码（Salt的相关代码见最后）：

#include <iostream>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void HarmonicMeanFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    // 以镜像复制扩充边界
    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    double k = m * n;
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            double sum = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                    sum += 1.0 / (input.at<uchar>(i + x, j + y) + 0.1);
            sum = k / sum;
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = sum;
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现方法
    HarmonicMeanFilter(input, output1, 7, 7);
    // OpenCV盒式滤波器
    cv::blur(input, output2, cv::Size(7, 7));

    cv::namedWindow("谐波均值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("谐波均值滤波器", output1);
    cv::namedWindow("算术均值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("算术均值滤波器", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

8.1.4 反谐波均值滤波器

反谐波均值滤波器：调节阶数有不同的效果，适用于降低或消除椒盐噪声，当阶数Q为正时，可消除胡椒噪声；当阶数Q为负时，可消除盐粒噪声；Q=0时简化为算术平均滤波器；Q=-1时简化为谐波平均滤波器。表达式如下，其中 $\hat f$ 为复原的图像， $S_{xy}$ 表示中心为(x,y)、大小为m×n的矩形子图像窗口的一组坐标， $g(x,y)$ 为被污染的图像：

\hat f(x,y)=\frac{\sum_{(r,c)\in S_{xy} }g(r,c)^{Q+1} } {\sum_{(r,c)\in S_{xy} }g(r,c)^Q}

代码（Salt的相关代码见最后）：

#include <iostream>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void AntiharmonicAveragingFilter(cv::Mat input, cv::Mat &output, int m, int n, int q)
{
    output = input.clone();
    // 以镜像复制扩充边界
    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);


    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            double sum1 = 0, sum2 = 0, sum;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    sum1 += pow(input.at<uchar>(i + x, j + y), q + 1);
                    sum2 += pow(input.at<uchar>(i + x, j + y), q);
                }
            sum = sum1 / sum2;
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = cv::saturate_cast<uchar>(sum);
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现方法
    AntiharmonicAveragingFilter(input, output1, 7, 7, 2);
    AntiharmonicAveragingFilter(input, output2, 7, 7, -2);

    cv::namedWindow("反谐波均值滤波器：Q=2", cv::WINDOW_NORMAL);
    cv::imshow("反谐波均值滤波器：Q=2", output1);
    cv::namedWindow("反谐波均值滤波器：Q=-2", cv::WINDOW_NORMAL);
    cv::imshow("反谐波均值滤波器：Q=-2", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

#pragma once
#include <opencv2/opencv.hpp>
#include <random>

void Salt(cv::Mat input, int n);

//Salt.cpp
#include "Salt.h"

void Salt(cv::Mat input, int n)
{
    std::default_random_engine generator;
    std::uniform_int_distribution<int>row(0, input.rows - 1);
    std::uniform_int_distribution<int>col(0, input.cols - 1);
    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = row(generator);
        j = col(generator);
        if (input.channels() == 1)
            input.at<uchar>(i, j) = 255;
        else if (input.channels() == 3)
            input.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 255, 255);
    }
}

8.2 统计排序滤波器

8.2.1 中值滤波器

处理单极、双极冲激噪声更好，也能有效降低某些随机噪声，丢失细节更少。表达式如下，其中 $\hat f$ 为复原的图像， $S_{xy}$ 是中心为(x,y)的子图像， $g(x,y)$ 为被污染的图像：

\hat f(x,y)=median_{(r,c)\in S_{xy} }\{g(r,c)\}

代码实现：

#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void MedianFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = arry[(num - 1) / 2];
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现中值滤波器
    MedianFilter(input, output1, 7, 7);
    // OpenCV自带中值滤波器
    cv::medianBlur(input, output2, 7);

    cv::namedWindow("自实现中值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("自实现中值滤波器", output1);
    cv::namedWindow("OpenCV自带中值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("OpenCV自带中值滤波器", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

8.2.2 最大值滤波器

滤波窗口的最大值作为滤波结果，可通过最大值滤波器削减胡椒噪声，也可削弱明色区域相邻的暗色区域。其中 $\hat f$ 为复原的图像， $S_{xy}$ 是中心为(x,y)的子图像， $g(x,y)$ 为被污染的图像：

\hat f(x,y)=\max_{(r,c)\in S_{xy} }\{g(r,c)\}

代码实现：

#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void MaxFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = arry[num - 1];
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output;

    Salt(input, 100000);    // 给图片添加10w个黑色噪点（胡椒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    MaxFilter(input, output, 7, 7);

    cv::namedWindow("最大值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("最大值滤波器", output);

    cv::waitKey(0);
    return 0;
}

效果展示：

8.2.3 最小值滤波器

滤波窗口的最小值作为滤波结果，可通过最小值滤波器削减盐粒噪声，也可削弱暗色区域相邻的明色区域。表达式如下，其中 $\hat f$ 为复原的图像， $S_{xy}$ 是中心为(x,y)的子图像， $g(x,y)$ 为被污染的图像：

\hat f(x,y)=\min_{(r,c)\in S_{xy} }\{g(r,c)\}

代码实现：

#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void MinFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = arry[0];
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    MinFilter(input, output, 7, 7);

    cv::namedWindow("最小值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("最小值滤波器", output);

    cv::waitKey(0);
    return 0;
}

效果展示：

8.2.4 中点滤波器

滤波窗口的最大值和最小值的均值作为滤波结果，适合处理随机分布的噪声，如高斯噪声和均匀噪声。表达式如下，其中 $\hat f$ 为复原的图像， $S_{xy}$ 是中心为(x,y)的子图像， $g(x,y)$ 为被污染的图像：

\hat f(x,y)=\frac 12\bigg[\max_{(r,c)\in S_{xy} }\{g(r,c)\}+\min_{(r,c)\in S_{xy} }\{g(r,c)\}\bigg]

代码实现：

#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void MidPointFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = round((arry[0] + arry[num - 1]) / 2);
        }

}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    MidPointFilter(input, output, 7, 7);

    cv::namedWindow("中点滤波器", cv::WINDOW_NORMAL);
    cv::imshow("中点滤波器", output);

    cv::waitKey(0);
    return 0;
}

效果展示：

不太适合盐粒噪声

8.2.5 修正阿尔法均值滤波器

假设要在邻域 $S_{xy}$ 内删除 $g(r,c)$ 的 $d$ 个最低灰度值和 $d$ 个最高灰度值。令 $g(r,c)$ 表示S中剩下的 $mn-2d$ 个像素，通过平均这些剩余像素所形成的滤波器，称为修正阿尔法均值滤波器。

当 $d=0$ 时简化为算术平均滤波器，当 $d=(mn-1)/2$ 时变成中值滤波器，当 $d$ 为其他值时适合处理多种混合噪声，如高斯噪声和椒盐噪声。

\hat f(x,y)=\frac{1} {mn-2d}\sum_{(r,c)\in S_{xy} }g_R(r,c)

代码实现：

#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void ModifiedAlphaMeanFilter(cv::Mat input, cv::Mat &output, int m, int n, int d)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x ++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            int sum = 0;
            for (int k = d; k < num - d - 1; k ++)
                sum += arry[k];
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = round(sum / (num - 2 * d));
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    ModifiedAlphaMeanFilter(input, output1, 7, 7, 3);
    ModifiedAlphaMeanFilter(input, output2, 7, 7, 9);

    cv::namedWindow("修正阿尔法均值滤波器：d=3", cv::WINDOW_NORMAL);
    cv::imshow("修正阿尔法均值滤波器：d=3", output1);
    cv::namedWindow("修正阿尔法均值滤波器：d=9", cv::WINDOW_NORMAL);
    cv::imshow("修正阿尔法均值滤波器：d=9", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

//Salt.h
#pragma once
#include <opencv2/opencv.hpp>
#include <random>

void Salt(cv::Mat input, int n);

#include "Salt.h"

void Salt(cv::Mat input, int n)
{
    std::default_random_engine generator;
    std::uniform_int_distribution<int>row(0, input.rows - 1);
    std::uniform_int_distribution<int>col(0, input.cols - 1);
    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = row(generator);
        j = col(generator);
        if (input.channels() == 1)
            input.at<uchar>(i, j) = 255; //试验最大值滤波器时取为0
        else if (input.channels() == 3)
            input.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 255, 255); //试验最大值滤波器时取为(0,0,0)
    }
}

8.3 自适应滤波器

8.3.1 自适应局部降噪滤波器

滤波器对中心(x,y)的一个邻域 $S_{xy}$ 进行操作，

噪声图像g(x,y)，噪声方差 $\sigma_\eta^2$ ；
$S_{xy}$ 中像素的平均灰度 $\overline{z}_{S_{xy} }$ ， $S_{xy}$ 中像素灰度的局部方差 $\sigma^2_{S_{xy} }$ ；

希望滤波器满足：

噪声为0时，(x,y)处的值g等于f。若噪声图像方差 $\sigma^2_\eta=0$ ，则滤波器仅返回(x,y)处的值g。
高局部方差通常与边缘相关，且应保留这些边缘。若局部方差 $\sigma^2_{S_{xy} }$ 与 $\sigma_\eta^2$ 高度相关，则滤波器返回(x,y)处一个接近于g的值。
当局部区域的性质与整个图像的性质相同时，则两个方差相等，滤波器返回 $S_{xy}$ 中像素的算术平均值，平均运算降低局部噪声。

处理步骤：

计算噪声图像方差 $\sigma^2_\eta$ ；
计算滤波器窗口内像素的均值 $z_{S_{sy} }$ 和方差 $\sigma^2_{S_{xy} }$ ；
利用下式计算：

\hat{f}(x,y)=g(x,y)-\frac{\sigma^2_{\eta} } {\sigma^2_{S_{xy} }}\big[g(x,y)-\overline{z_{S_{xy} }}\big],\frac{\sigma^2_{\eta} } {\sigma^2_{S_{xy} }}\leq1

代码：

涉及OpenCV函数：

1	void meanStdDev(InputArray src, OutputArray mean, OutputArray stddev, InputArray mask=noArray());

参数分别为：

src：输入矩阵
mean：输出均值
stddev：输出标准差
mask：可选参数，掩码

#include <iostream>
#include <opencv2/opencv.hpp>

// 添加高斯噪声
void GaussianNoise(cv::Mat input, cv::Mat &output)
{
    cv::RNG rng;
    cv::Mat noice = input.clone();
    output = input.clone();
    rng.fill(noice, cv::RNG::NORMAL, 10, 20);    // 使用NORMAL参数添加高斯噪声
    output = input + noice;
}

void AdaptiveLocalNoiseReductionFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    cv::Mat arry(1, m * n, CV_8U);    // 局部矩阵

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    cv::Mat mean1, stddev1, mean2, stddev2;
    cv::meanStdDev(input, mean1, stddev1);    // 获取矩阵平均值和标准差
    double _stddev1, _mean2, _stddev2;        // 图像标准差、局部均值和局部标准差
    _stddev1 = stddev1.at<double>(0, 0);

    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x ++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry.at<uchar>(h) = input.at<uchar>(i + x, j + y);
                    h ++;
                }

            cv::meanStdDev(arry, mean2, stddev2);
            _stddev2 = stddev2.at<double>(0, 0);
            _mean2 = mean2.at<double>(0, 0);

            double k = (_stddev1 * _stddev1) / (_stddev2 * _stddev2 + 0.00001);
            if (k <= 1)
                output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = input.at<uchar>(i, j) - k * (input.at<uchar>(i, j) - _mean2);
            else
                output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = _mean2;
        }

}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output;

    GaussianNoise(input, input);    //添加高斯噪声

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    AdaptiveLocalNoiseReductionFilter(input, output, 7, 7);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", output);


    cv::waitKey(0);
    return 0;
}

效果展示：

8.3.2 自适应中值滤波器

通过判断，将中值或者原像素灰度值作为结果。记以下符号：

$z_{min}$ 是 $S_{xy}$ 中的最小灰度值； $z_{max}$ 是 $S_{xy}$ 中的最大灰度值； $z_{med}$ 是 $S_{xy}$ 中灰度值的中值；

$z_{xy}$ 是坐标 $(x,y)$ 处的灰度值， $S_{max}$ 是 $S_{xy}$ 允许的最大尺寸。

代码：

#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

// 添加高斯噪声
void GaussianNoise(cv::Mat input, cv::Mat &output)
{
    cv::RNG rng;
    cv::Mat noice = input.clone();
    output = input.clone();
    rng.fill(noice, cv::RNG::NORMAL, 10, 50);    // 使用NORMAL参数添加高斯噪声
    output = input + noice;
}

// 求输出值
uchar AdaptiveMedian(cv::Mat input, int i, int j, int filter_size, int maxsize)
{
    int num = filter_size * filter_size;
    std::vector<uchar> arry(num);
    int h = 0;
    for (int x = -(filter_size - 1) / 2; x <= (filter_size - 1) / 2; x ++)
        for (int y = -(filter_size - 1) / 2; y <= (filter_size - 1) / 2; y ++)
        {
            arry[h] = input.at<uchar>(i + x, j + y);
            h ++;
        }
    sort(arry.begin(), arry.end());
    int z_min = arry[0];
    int z_med = arry[(num - 1) / 2];
    int z_max = arry[num - 1];
    int z_xy = input.at<uchar>(i, j);

    if (z_med > z_min and z_med < z_max)
    {
        if (z_xy > z_min and z_xy < z_max)
            return z_xy;
        else return z_med;
    }

    else
    {
        filter_size += 2;
        if (filter_size <= maxsize)
            return AdaptiveMedian(input, i, j, filter_size, maxsize);
        else return z_med;
    }
}

// 自适应中值滤波器
void AdaptiveMedianFilter(cv::Mat input, cv::Mat &output, int maxsize)
{
    output = input.clone();

    cv::copyMakeBorder(input, input, (maxsize - 1) / 2, (maxsize - 1) / 2, (maxsize - 1) / 2, (maxsize - 1) / 2, cv::BORDER_REFLECT);

    for (int i = (maxsize - 1) / 2; i < input.rows - (maxsize - 1) / 2; i ++)
        for (int j = (maxsize - 1) / 2; j < input.cols - (maxsize - 1) / 2; j ++)
        {
            int filter_size = 3;    // 开始时滤波器尺寸
            output.at<uchar>(i - (maxsize - 1) / 2, j - (maxsize - 1) / 2) = AdaptiveMedian(input, i, j, filter_size, maxsize);
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    cv::Mat noise1 = input.clone(), noise2 = input.clone();

    GaussianNoise(input, noise1);    // 添加高斯噪声
    Salt(input, noise2, 100000);            // 添加盐粒噪声

    cv::namedWindow("高斯噪声", cv::WINDOW_NORMAL);
    cv::imshow("高斯噪声", noise1);
    cv::namedWindow("盐粒噪声", cv::WINDOW_NORMAL);
    cv::imshow("盐粒噪声", noise2);

    AdaptiveMedianFilter(noise1, output1, 7);
    AdaptiveMedianFilter(noise2, output2, 7);

    cv::namedWindow("降低高斯噪声", cv::WINDOW_NORMAL);
    cv::imshow("降低高斯噪声", output1);
    cv::namedWindow("降低盐粒噪声", cv::WINDOW_NORMAL);
    cv::imshow("降低盐粒噪声", output2);


    cv::waitKey(0);
    return 0;
}

// Salt.h
#pragma once
#include <opencv2/opencv.hpp>
#include <random>

void Salt(cv::Mat input, cv::Mat &output, int n);

// Salt.cpp
#include "Salt.h"

void Salt(cv::Mat input, cv::Mat &output, int n)
{
    output = input.clone();
    std::default_random_engine generator;
    std::uniform_int_distribution<int>row(0, input.rows - 1);
    std::uniform_int_distribution<int>col(0, input.cols - 1);
    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = row(generator);
        j = col(generator);
        if (input.channels() == 1)
            output.at<uchar>(i, j) = 255;
        else if (input.channels() == 3)
            output.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 255, 255);
    }
}

效果展示；

对于盐粒噪声有奇效

九、彩色图像处理基础

9.1 彩色图像基础

颜色的特性可以表达成亮度、色调和饱和度。

亮度：即强度，如灰度值
色调：混合在光波中的主导光波属性，即被观察者感知的主导色。
饱和度：相对的纯度，或与一种色调混合的白光量。比如浅红色（红色+白色）是不饱和的，白色越多，越不饱和。

色度=色调+饱和度，颜色=亮度+色度

9.2 彩色图像模型

常见的彩色图像模型有：

RGB（红绿蓝）：一般用于彩色显示器和彩色摄影机。
CMY（青、深红、黄）和CMYK（青、深红、黄、黑）：一般用于彩色打印。
HSI（色调、饱和度、亮度）：描述和解释颜色

9.3 RGB模型与HSI模型之间的转换

9.3.1 从RGB到HSI

此处HSI的计算假设RGB已被归一化到[0,1]，且θ是相对于HSI空间的红色轴测量，得到的HSI结果也在区间[0,1]中。

H色调分量计算：

H=\begin{cases} \theta & if\ B\leq G\\ 360-\theta & if\ B >G \end{cases}

\theta=cos^{-1}\frac{\frac{1} {2}[(R-G)+(R+B)]} {[(R-G)^2+(R-B)(G-B)]^{1/2} }

S饱和度分量计算：

S=1-\frac{3} {R+G+B}[\min(R,G,B)]

I亮度分量计算：

I=\frac 13(R+G+B)

9.3.2 从HSI到RGB

值区间同上[0,1]

先计算H色调值，再根据H的范围使用不同的公式。

把H值从[0,1]转换到[0,360]：

H=H\times 360°

根据H的范围使用不同计算公式：

当 $H\in[0,120)$ ，即RG扇区：

\left\{ \begin{matrix} B&=&I(1-S) \\ R&=&I[1+\frac{S\cos H} {\cos(60°-H)}]\\ G&=&3I-(R+B) \end{matrix} \right.

当 $H\in[120,240)$ ，即GB扇区：

\left\{ \begin{matrix} H&=&H-120°\\ B&=&I(1-S) \\ R&=&I[1+\frac{S\cos H} {\cos(60°-H)}]\\ G&=&3I-(R+B) \end{matrix} \right.

当 $H\in[240,360]$ ，即GB扇区：

\left\{ \begin{matrix} H&=&H-240°\\ B&=&I(1-S) \\ R&=&I[1+\frac{S\cos H} {\cos(60°-H)}]\\ G&=&3I-(R+B) \end{matrix} \right.

十、图像形态学处理

10.1 腐蚀

定义B对A的腐蚀为：

A\ominus B = \{z|(B)_z\subseteq A\}

其中，A是前景像素的一个集合，B是一个结构元，z项是前景像素值。

腐蚀的目的是去除图像中的某些部分以及会缩小细化目标。

但是，对于白色背景，黑色目标变大；对于黑色背景，白色目标变小。

可以理解为结构元像素是白色的，腐蚀是腐蚀图像中的白色像素，白色像素被腐蚀，则黑色元素膨胀。

代码如下：

10.2 膨胀

定义B对A的腐蚀为：

A\oplus B = \{z|[(\hat{B})_z\cap A]\subseteq A \}

其中，A是前景像素的一个集合，B是一个结构元，z项是前景像素值。

腐蚀的目的是增大图像中的目标，或者填充、连接某些目标。

但是，对于白色背景，黑色目标变小；对于黑色背景，白色目标变大。

可以理解为结构元像素是白色的，膨胀是膨胀图像中的白色像素，白色像素被膨胀，则黑色元素腐蚀。

代码如下：

10.3 开运算与闭运算

结构元B对集合A的开运算定义为：

A\circ B=(A\ominus B)\oplus B

即B对A先腐蚀，接着B对腐蚀结果膨胀。

作用是：平滑物体轮廓、断开狭窄的狭颈、消除细长的突出和物体。

结构元B对集合A的闭运算定义为：

A\bullet B=(A\oplus B)\ominus B

即B对A先膨胀，接着B对膨胀结果腐蚀。

作用是：弥合狭窄的狭颈或断裂处、消除小孔、填补轮廓缝隙。

代码如下：

#include <opencv2/opencv.hpp>

void imageOpenOperation(cv::Mat input, cv::Mat &output)
{
    output = input.clone();
    cv::Mat se = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(3, 3));
    cv::erode(input, output, se);
    cv::dilate(output, output, se);
}

void imageCloseOperation(cv::Mat input, cv::Mat &output)
{
    output = input.clone();
    cv::Mat se = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(3, 3));
    cv::dilate(input, output, se);
    cv::erode(output, output, se);
}

int main()
{
    cv::Mat input = cv::imread("src/pic2.png", 0);
    cv::Mat img_bw, result1, result2;    // 二值化后的图像、开运算结果、比运算结果
    cv::threshold(input, img_bw, 100, 255, cv::THRESH_BINARY);    // 二值化

    imageOpenOperation(img_bw, result1);
    imageCloseOperation(img_bw, result2);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::namedWindow("开运算后", cv::WINDOW_NORMAL);
    cv::namedWindow("闭运算后", cv::WINDOW_NORMAL);

    cv::imshow("before", img_bw);
    cv::imshow("开运算后", result1);
    cv::imshow("闭运算后", result2);

    cv::waitKey(0);
    return 0;
}

10.4 morphologyEx()函数的运用

膨胀腐蚀、开运算闭运算、击中-击不中变换、顶帽变换与底帽变换、形态学梯度

10.4.1 相关函数原型

void morphologyEx(  InputArray src,
                    OutputArray dst,
                    int op, 
                    InputArray kernel,
                    Point anchor = Point(-1,-1), 
                    int iterations = 1,
                    int borderType = BORDER_CONSTANT,
                    const Scalar& borderValue = morphologyDefaultBorderValue() );

参数如下：

src：输入图像，图像数据类型必须为CV_8U, CV_16U, CV_16S, CV_32F or CV_64F中的一种。
dst：输出图像，数据类型与大小和输入图像一样。
op：形态学处理的类型。

MORPH_ERODE = 0：腐蚀处理

MORPH_DILATE = 1：膨胀处理

MORPH_OPEN = 2：开运算处理

MORPH_CLOSE = 3：闭运算处理

MORPH_GRADIENT = 4：形态学梯度

MORPH_TOPHAT = 5：顶帽变换

MORPH_BLACKHAT = 6：黑帽变换

MORPH_HITMISS = 7 ：击中-击不中变换

kernel：结构元矩阵。
iterations：腐蚀膨胀处理的次数，默认值为1；如果是开运算闭运算，次数表示先腐蚀或者膨胀几次，再膨胀腐蚀几次，而不是开运算闭运算几次。
borderType：图像边框插值类型，默认类型为固定值填充。
borderValue：边界值（如果是恒定边界）。默认值具有特殊含义。

10.4.2 进行腐蚀膨胀

#include <opencv2/opencv.hpp>

int main()
{
    cv::Mat input = cv::imread("src/pic2.png", 0);
    cv::Mat img_bw, result1, result2;
    cv::threshold(input, img_bw, 100, 255, cv::THRESH_BINARY);    // 二值化

    cv::Mat kernel = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(3, 3));
    cv::morphologyEx(img_bw, result1, 0, kernel);    // 腐蚀
    cv::morphologyEx(img_bw, result2, 1, kernel);    // 膨胀

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::namedWindow("腐蚀结果", cv::WINDOW_NORMAL);
    cv::namedWindow("膨胀结果", cv::WINDOW_NORMAL);

    cv::imshow("before", img_bw);
    cv::imshow("腐蚀结果", result1);
    cv::imshow("膨胀结果", result2);

    cv::waitKey(0);
    return 0;
}

效果展示：

10.4.3 进行开运算和闭运算

#include <opencv2/opencv.hpp>

int main()
{
    cv::Mat input = cv::imread("src/pic2.png", 0);
    cv::Mat img_bw, result1, result2;
    cv::threshold(input, img_bw, 100, 255, cv::THRESH_BINARY);    // 二值化

    cv::Mat kernel = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(3, 3));
    cv::morphologyEx(img_bw, result1, 2, kernel);    // 开运算
    cv::morphologyEx(img_bw, result2, 3, kernel);    // 闭运算

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::namedWindow("开运算结果", cv::WINDOW_NORMAL);
    cv::namedWindow("闭运算结果", cv::WINDOW_NORMAL);

    cv::imshow("before", img_bw);
    cv::imshow("开运算结果", result1);
    cv::imshow("闭运算结果", result2);

    cv::waitKey(0);
    return 0;
}

效果展示：

10.4.4 击中-击不中变换

原理：

I\circledast B=\{z|(B)_z\subseteq I\}

可以检测图像中满足结构元B的所有像素点，如：

图中结构元B中深色像素为前景，白色表示为背景， × 表示不关心像素（即不影响结果）。

击中-击不中变换是形状检测的基本工具，寻找与结构元相符合的像素。

在击中击不中变换的结构元中，-1表示背景，1表示前景，0表示不关心。

代码如下：

#include <opencv2/opencv.hpp>

int main()
{
    cv::Mat input = cv::imread("src/rice.jpg", 0);
    cv::Mat img_bw, result;
    cv::threshold(input, img_bw, 100, 255, cv::THRESH_BINARY);    // 二值化

    cv::Mat kernel = (cv::Mat_<float>(3, 3) << 1, 1, -1, 1, 1, -1, 1, 1, -1);

    cv::morphologyEx(img_bw, result, 7, kernel);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::namedWindow("击中-击不中变换结果", cv::WINDOW_NORMAL);

    cv::imshow("before", img_bw);
    cv::imshow("击中-击不中变换结果", result);

    cv::waitKey(0);
    return 0;
}

效果展示：

10.4.5 顶帽变换与底帽变换

顶帽变换（礼帽变换）

是原图像与开运算结果图之差。
作用：提取出细线状的部分或者噪声。

底帽变换（黑帽变换）

是闭运算与原图像结果图之差。
作用：得到图像内部的小孔，或前景色的小黑点。

代码如下：

#include <opencv2/opencv.hpp>

int main()
{
    cv::Mat input = cv::imread("src/rice.jpg", 0);
    cv::Mat img_bw, result1, result2;
    cv::threshold(input, img_bw, 100, 255, cv::THRESH_BINARY);
    cv::Mat kernel = cv::getStructuringElement(0, cv::Size(5, 5));

    cv::morphologyEx(img_bw, result1, 5, kernel);
    cv::morphologyEx(img_bw, result2, 6, kernel);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::namedWindow("顶帽变换结果", cv::WINDOW_NORMAL);
    cv::namedWindow("底帽变换结果", cv::WINDOW_NORMAL);

    cv::imshow("before", img_bw);
    cv::imshow("顶帽变换结果", result1);
    cv::imshow("底帽变换结果", result2);

    cv::waitKey(0);
    return 0;
}

效果截图：

10.4.6 形态学梯度

膨胀图与腐蚀图之差；
对二值图进行这一操作可以得到图像中白色区域的边界，因此可以用形态学梯度来保留物体的边界轮廓。

代码如下：

#include <opencv2/opencv.hpp>

int main()
{
    cv::Mat input = cv::imread("src/pic2.png", 0);
    cv::Mat img_bw, result;
    cv::threshold(input, img_bw, 100, 255, cv::THRESH_BINARY_INV);
    cv::Mat kernel = cv::getStructuringElement(0, cv::Size(5, 5));

    cv::morphologyEx(img_bw, result, 4, kernel);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::namedWindow("形态学梯度结果", cv::WINDOW_NORMAL);

    cv::imshow("before", img_bw);
    cv::imshow("形态学梯度结果", result);

    cv::waitKey(0);
    return 0;
}

效果截图：

10.5 提取连通域

连通域：指图像中具有相同像素值且位置相邻的像素组成的区域。

10.5.1 connectedComponents函数

1	int connectedComponents(InputArray image, OutputArray labels, int connectivity = 8, int ltype = CV_32S);

参数如下：

image：输入图像，待标记8位单通道图像。
labels：输出图像，目标标记图像。
connectivity：连通域大小，四连通域还是八连通域。
输出类型：CV32S 和 CV_16U ，默认是 CV_32S 。
返回连通域个数。

代码如下：

#include <opencv2/opencv.hpp>
#include <iostream>

int main()
{
    cv::Mat input = cv::imread("src/rice.jpg");
    cv::Mat img_bw, connectimg;
    cv::cvtColor(input, img_bw, cv::COLOR_BGR2GRAY);
    cv::threshold(img_bw, img_bw, 100, 255, cv::THRESH_BINARY_INV);

    // 做一些膨胀和腐蚀使得图像连通域明显
    cv::Mat element = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(5, 5));
    cv::erode(img_bw, img_bw, element, cv::Point(-1, -1), 2);
    cv::dilate(img_bw, img_bw, element, cv::Point(-1, -1), 2);

    int num = cv::connectedComponents(img_bw, connectimg, 8, CV_16U);
    std::cout << "连通域个数：" << num << std::endl;

    cv::namedWindow("原图", cv::WINDOW_NORMAL);
    cv::imshow("原图", img_bw);

    //以不同颜色标记出不同的连通域
    cv::Mat result = cv::Mat::zeros(img_bw.size(), CV_8UC3); //定义标记结果图像
    //定义五种颜色
    std::vector<cv::Vec3b> color;
    color.push_back(cv::Vec3b(0, 0, 255));
    color.push_back(cv::Vec3b(0, 255, 0));
    color.push_back(cv::Vec3b(255, 0, 0));
    color.push_back(cv::Vec3b(0, 255, 255));
    color.push_back(cv::Vec3b(255, 255, 0));

    for (int i = 0; i < result.cols; i ++)
    {
        for (int j = 0; j < result.rows; j ++)
        {
            int label = connectimg.at<uint16_t>(i, j);
            if (label == 0)
            {
                continue;    //背景的黑色不改变
            }
            result.at<cv::Vec3b>(i, j) = color[label % 5];
        }
    }

    cv::namedWindow("标记连通域后", cv::WINDOW_NORMAL);
    cv::imshow("标记连通域后", result);

    cv::waitKey(0);
    return 0;
}

效果截图：

注：黑色也算一个连通域

10.5.2 connectedComponentsWithStats函数

函数：

1	int connectedComponentsWithStats(InputArray image, OutputArray labels, OutputArray stats, OutputArray centroids, int connectivity = 8, int ltype = CV_32S);

参数如下：

image：要标记的8位单通道图像
labels：目标标签图像
stats：每个标签的统计输出，是一个5列的矩阵，每一行对应每个连通区域的外接矩形的左上角坐标x、y，以及外接矩形的宽高width、height和面积area。
centroids：连通域中心点，数据类型CV_64F。
connectivity：8或4分别用于八连通域和四连通域。
ltype输出图像标签类型。目前支持CV_32S和CV_16U。
返回连通域个数。

其中， stats包含了标签为i的连通域的一些信息，可以如下访问标签为i的连通域的面积：

1	stats.at<int>(i, CC_STAT_AREA)

连通域外接矩形的参数：

// 矩形左上角x
x = stats.at<int>(max_idx, cv::CC_STAT_LEFT);
// 矩形左上角y
y = stats.at<int>(max_idx, cv::CC_STAT_TOP);
// 矩形高
h = stats.at<int>(max_idx, cv::CC_STAT_HEIGHT);
// 矩形宽
w = stats.at<int>(max_idx, cv::CC_STAT_WIDTH);

十一、图像分割

11.1 图像边缘检测

11.1.1边缘检测的步骤

为了降低噪声，对图像进行平滑处理。
检测边缘点。
边缘定位。

11.1.2 图像梯度

计算图像f在任意位置(x, y)处的边缘强度和方向的工具是梯度。

定义梯度为向量：

\nabla f(x,y)\equiv grad[f(x,y)]\equiv \left[ \begin{matrix} g_x(x,y)\\ g_y(x,y)\\ \end{matrix} \right]= \left[ \begin{matrix} \frac{\partial f(x,y)} {\partial x}\\ \frac{\partial f(x,y)} {\partial y}\\ \end{matrix} \right]

根据梯度向量求点(x,y)处方向变化率的值：

M(x,y) = \vert\vert\nabla f(x,y)\vert\vert=\sqrt{g_x^2(x,y)+g_y^2(x,y)}

其中M(x,y)称为图像f的梯度图像。

上式变化率方向为：

\alpha(x,y)=\tan^{-1}\Big[\frac{g_y(x,y)} {g_x(x,y)}\Big]

常见梯度算子有：

前向差分：有一维核也有二维核（Roberts核）

g_x(x,y)=\frac{\partial f(x,y)} {\partial x}=f(x+1,y)-f(x,y)

g_y(x,y)=\frac{\partial f(x,y)} {\partial y}=f(x,y+1)-f(x,y)

中心有限差分：常见有Prewitt核核Sobel核

11.1.3 点检测

使用拉普拉斯核进行孤立点检测。

11.1.4 线检测

同样可以使用拉普拉斯核进行线检测，但也有规定方向的线检测。

11.1.5 Roberts边缘检测

部分代码如下：

cv::Mat kernel1 = (cv::Mat_<float>(2, 2) << -1, 0, 0, 1 );
cv::Mat kernel2 = (cv::Mat_<float>(2, 2) << 0, -1, 1, 0 );

cv::filter2D(src, dst1, -1, kernel1);    // 方向1
cv::filter2D(src, dst2, -1, kernel2);    // 方向2

cv::convertScaleAbs(dst1, dst1);    // 取绝对值
cv::convertScaleAbs(dst2, dst2);    // 取绝对值

dst = dst1 + dst2;  // 合并

11.1.6 Prewitt边缘检测

部分代码如下：

cv::Mat kernel1 = (cv::Mat_<float>(3, 3) << -1, -1, -1, 0, 0, 0, 1, 1, 1);
cv::Mat kernel2 = (cv::Mat_<float>(3, 3) << -1, 0, 1, -1, 0, 1, -1, 0, 1);

cv::filter2D(src, dst1, -1, kernel1);    // 方向1
cv::filter2D(src, dst2, -1, kernel2);    // 方向2

cv::convertScaleAbs(dst1, dst1);    // 取绝对值
cv::convertScaleAbs(dst2, dst2);    // 取绝对值

dst = dst1 + dst2;  // 合并

11.1.7 Sobel边缘检测

部分代码如下：

cv::Mat kernel1 = (cv::Mat_<float>(3, 3) << -1, -2, -1, 0, 0, 0, 1, 2, 1);
cv::Mat kernel2 = (cv::Mat_<float>(3, 3) << -1, 0, 1, -2, 0, 2, -1, 0, 1);

cv::filter2D(src, dst1, -1, kernel1);    // 方向1
cv::filter2D(src, dst2, -1, kernel2);    // 方向2

cv::convertScaleAbs(dst1, dst1);    // 取绝对值
cv::convertScaleAbs(dst2, dst2);    // 取绝对值

dst = dst1 + dst2;  // 合并

11.1.8 Kirsch边缘检测

部分代码如下：

cv::Mat kernel1 = (cv::Mat_<float>(3, 3) << -3, -3, 5, -3, 0, 5, -3, -3, 5);
cv::Mat kernel2 = (cv::Mat_<float>(3, 3) << 5, -3, -3, 5, 0, -3, 5, -3, -3);
cv::Mat kernel3 = (cv::Mat_<float>(3, 3) << 5, 5, 5, -3, 0, -3, -3, -3, -3);
cv::Mat kernel4 = (cv::Mat_<float>(3, 3) << -3, -3, -3, -3, 0, -3, 5, 5, 5);
cv::Mat kernel5 = (cv::Mat_<float>(3, 3) << -3, 5, 5, -3, 0, 5, -3, -3, -3);
cv::Mat kernel6 = (cv::Mat_<float>(3, 3) << 5, 5, -3, 5, 0, -3, -3, -3, -3);
cv::Mat kernel7 = (cv::Mat_<float>(3, 3) << -3, -3, -3, -3, 0, 5, -3, 5, 5);
cv::Mat kernel8 = (cv::Mat_<float>(3, 3) << -3, -3, -3, 5, 0, -3, 5, 5, -3);

cv::filter2D(src, dst1, -1, kernel1);    // 方向1
cv::filter2D(src, dst2, -1, kernel2);    // 方向2
cv::filter2D(src, dst3, -1, kernel3);    // 方向3
cv::filter2D(src, dst4, -1, kernel4);    // 方向4
cv::filter2D(src, dst5, -1, kernel5);    // 方向5
cv::filter2D(src, dst6, -1, kernel6);    // 方向6
cv::filter2D(src, dst7, -1, kernel7);    // 方向7
cv::filter2D(src, dst8, -1, kernel8);    // 方向8

cv::convertScaleAbs(dst1, dst1);
cv::convertScaleAbs(dst2, dst2);
cv::convertScaleAbs(dst3, dst3);
cv::convertScaleAbs(dst4, dst4);
cv::convertScaleAbs(dst5, dst5);
cv::convertScaleAbs(dst6, dst6);
cv::convertScaleAbs(dst7, dst7);
cv::convertScaleAbs(dst8, dst8);

dst = src.clone();
for (int i = 0; i < src.rows; i++)
    for (int j = 0; j < src.cols; j++)
    {
        int arr[] = { dst1.at<uchar>(i, j), dst2.at<uchar>(i, j)
            , dst3.at<uchar>(i, j), dst4.at<uchar>(i, j), dst5.at<uchar>(i, j)
            , dst6.at<uchar>(i, j), dst7.at<uchar>(i, j), dst8.at<uchar>(i, j) };
        std::sort(arr, arr + 8);
        int max_num = arr[7];
        dst.at<uchar>(i, j) = max_num;  // 取8个方向的最大值作为结果
    }

11.1.9 LOG边缘检测

高斯拉普拉斯LOG函数：

\nabla^2G(x,y)=(\frac{x^2+y^2-2\sigma^2} {\sigma^4})e^{-\frac{x^2+y^2} {2\sigma^2} }

其由拉普拉斯算子核高斯函数组成：

拉普拉斯算子：\nabla^2f=\frac{\partial^2f} {\partial x^2} + \frac{\partial^2f} {\partial y^2}

高斯函数：G(x,y)=e^{-\frac{x^2+y^2} {2\sigma^2} }

\nabla^2G(x,y)=\frac{\partial^2G(x,y)} {\partial x^2} + \frac{\partial^2G(x,y)} {\partial y^2}

构建LOG核的方法有两种：

由LOG函数进行计算（取样后要标定系数使系数和为0）；
构建高斯核，接着用拉普拉斯核进行卷积得到LOG核。

由于拉普拉斯和高斯是线性运算，使用LOG对图像进行边缘检测也有两种方法：

直接用LOG核对图像进行卷积。

g(x,y)=[\nabla^2G(x,y)]\star f(x,y)

先对图像进行高斯滤波，再对滤波后图像进行拉普拉斯变换。

g(x,y)=\nabla^2[G(x,y)\star f(x,y)]

代码如下：

#include <opencv2/opencv.hpp>

void LOG1(cv::Mat input, cv::Mat &output)
{
    output = input.clone();
    cv::Mat kernel = (cv::Mat_<float>(5, 5) <<
        0, 0, 1, 0, 0,
        0, 1, 2, 1, 0,
        1, 2, -16, 2, 1,
        0, 1, 2, 1, 0,
        0, 0, 1, 0, 0); // LOG核
    cv::filter2D(input, output, -1, kernel);
}

void LOG2(cv::Mat input, cv::Mat &output)
{
    output = input.clone();
    cv::GaussianBlur(input, output, cv::Size(5, 5), 1, 1);
    cv::Laplacian(output, output, input.depth(), 3, 1, 0, cv::BORDER_DEFAULT);
}

int main()
{
    cv::Mat src = cv::imread("src/lena.jpg");
    cv::Mat dst1, dst2;
    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    LOG1(src, dst1);
    LOG2(src, dst2);

    cv::namedWindow("原图", cv::WINDOW_NORMAL);
    cv::namedWindow("LOG1", cv::WINDOW_NORMAL);
    cv::namedWindow("LOG2", cv::WINDOW_NORMAL);
    cv::imshow("原图", src);
    cv::imshow("LOG1", dst1);
    cv::imshow("LOG2", dst2);

    cv::waitKey(0);
    return 0;
}

效果截图：

11.1.10 Canny边缘检测

Canny检测是传统边缘检测算子中最优秀的，基于：

低错误率。所有边缘都应该找到，没有虚假边缘。
准确的定位边缘。检测到的边缘是接近真实的边缘。
单个边缘点响应。只返回单点厚度的结果。

Canny边缘检测的步骤

①使用高斯滤波器平滑图像

void Gaussfilter(cv::Mat input, cv::Mat &output, int size, double sigma)
{
    // 处理核大小
    if (size < 3) size = 3;
    else size = static_cast<int>((size / 2) * 2 + 1);

    // 创建高斯核
    double **Gausskernel = new double *[size];
    for (int i = 0; i < size; i ++)
        Gausskernel[i] = new double[size];
    int center = size / 2;
    double sum = 0;

    for (int i = 0; i < size; i ++)
        for (int j = 0; j < size; j ++)
        {
            Gausskernel[i][j] = exp(-((i - center) * (i - center) + (j - center) * (j - center)) / (2 * sigma * sigma));
            sum += Gausskernel[i][j];
        }

    sum = 1.0 / sum;

    for (int i = 0; i < size; i ++)
        for (int j = 0; j < size; j ++)
            Gausskernel[i][j] *= sum;

    // 高斯滤波
    output = input.clone();
    for (int i = center; i < input.rows - center; i ++)
        for (int j = center; j < input.cols - center; j ++)
        {
            double sum = 0;
            for (int x = -center; x <= center; x ++)
                for (int y = -center; y <= center; y ++)
                    sum += Gausskernel[x + center][y + center] * input.at<uchar>(i + x, j + y);
            output.at<uchar>(i, j) = sum;
        }

    // 释放空间
    for (int i = 0; i < size; i ++) delete[] Gausskernel[i];
    delete[] Gausskernel;
}

②计算梯度幅值和边缘方向

使用Prewitt算子计算梯度。

计算梯度也有两种方式：

G=\sqrt{G_x^2+G_y^2}

G=G_x+G_y

根据边缘方向的法线方向确定边缘方向：

\alpha(x,y)=\arctan\Big[\frac{G_y(x,y)} {G_x(x,y)}\Big]

然后根据法线方向将边缘分为四个方向：水平、垂直、45°、-45°。有：

当法线方向为-22.5°~22.5°，或-157.5°~157.5°，则认为边缘为水平边缘；
当法线方向为22.5°~67.5°，或-112.5°~-157.5°，则认为边缘为-45°边缘；
当法线方向为67.5°~112.5°，或-67.5°~-112.5°，则认为边缘为垂直边缘；
当法线方向为112.5°~157.5°，或-22.5°~-67.5°，则认为边缘为45°边缘；

void GradDire(cv::Mat input, cv::Mat &Gradimg, cv::Mat &Direimg)
{
    Gradimg = cv::Mat(input.size(), CV_16U, cv::Scalar(0));
    Direimg = cv::Mat(input.size(), CV_8U, cv::Scalar(0));

    for (int i = 1; i < input.rows - 1; i++)
        for (int j = 1; j < input.cols - 1; j++)
        {
            // 计算梯度及梯度幅值
            int gx = input.at<uchar>(i + 1, j - 1) + input.at<uchar>(i + 1, j) + input.at<uchar>(i + 1, j + 1)
                - input.at<uchar>(i - 1, j - 1) - input.at<uchar>(i - 1, j) - input.at<uchar>(i - 1, j + 1);
            int gy = input.at<uchar>(i - 1, j + 1) + input.at<uchar>(i, j + 1) + input.at<uchar>(i + 1, j + 1)
                - input.at<uchar>(i - 1, j - 1) - input.at<uchar>(i, j - 1) - input.at<uchar>(i + 1, j - 1);
            int sum = gx + gy;
            Gradimg.at<ushort>(i, j) = std::abs(sum);

            // 方向图像，图像中的坐标轴，1-水平，2-45°，3-垂直，4--45°
            double dire = atan2(gy, gx) * 180 / 3.1415926;
            if (dire <= -67.5 or dire > 67.5)    Direimg.at<uchar>(i, j) = 1;
            else if (dire > -67.5 and dire < -22.5) Direimg.at<uchar>(i, j) = 2;
            else if (dire > -22.5 and dire < 22.5)    Direimg.at<uchar>(i, j) = 3;
            else Direimg.at<uchar>(i, j) = 4;
        }
}

③非极大值抑制

非极大值抑制原理为：在一个3*3的邻域内，根据边缘法线方向，与法线方向上其他两个邻点的梯度幅值比较大小，若该点大于另外两个邻点，则认为该点是边缘点，否则抑制。

void NonMaxSuppression(cv::Mat Gradimg, cv::Mat Direimg, cv::Mat &Suppimg)
{
    Suppimg = cv::Mat(Gradimg.size(), Gradimg.type(), cv::Scalar(0));

    for (int i = 1; i < Gradimg.rows - 1; i++)
        for (int j = 1; j < Gradimg.cols - 1; j++)
        {
            switch (Direimg.at<uchar>(i, j))
            {
                case 1:
                    if (Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i, j - 1) && Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i, j + 1))
                        Suppimg.at<ushort>(i, j) = Gradimg.at<ushort>(i, j);
                    else
                        Suppimg.at<ushort>(i, j) = 0;
                    break;
                case 2:
                    if (Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i + 1, j - 1) && Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i - 1, j + 1))
                        Suppimg.at<ushort>(i, j) = Gradimg.at<ushort>(i, j);
                    else
                        Suppimg.at<ushort>(i, j) = 0;
                    break;
                case 3:
                    if (Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i - 1, j) && Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i + 1, j))
                        Suppimg.at<ushort>(i, j) = Gradimg.at<ushort>(i, j);
                    else
                        Suppimg.at<ushort>(i, j) = 0;
                    break;
                case 4:
                    if (Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i - 1, j - 1) && Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i + 1, j + 1))
                        Suppimg.at<ushort>(i, j) = Gradimg.at<ushort>(i, j);
                    else
                        Suppimg.at<ushort>(i, j) = 0;
                    break;
                default:
                    break;
            }
        }
}

④使用双阈值处理和连通性分析检测和链接边缘

只设置一个阈值时，若阈值设置太低，则会出现假边缘；若阈值设置太高，则一些弱边缘会被丢弃。

步骤：

设置两个阈值：高阈值Th和低阈值Tl，一般高比低为2:1到3:1。
分别用这两个阈值对非极大值抑制图像进行阈值处理得到二值图像BWh和BWl，其中BWl的非零像素包含BWh。
分为强边缘图像和弱边缘图像，令BWl = BWh - BWl。此时认为BWh为强边缘图像，BWl为弱边缘图像。
标记弱边缘图像的真实边缘：在BWh中定位下一个没有被访问过的边缘像素P；在BWl中，认为P点坐标的8邻域内的弱边缘像素为真实边缘病标记；若BWh中所有像素均被访问，则结束，否则继续标记。

void doubleThread(cv::Mat Suppimg, cv::Mat &Edgeimg, int Tl, int Th)
{
    if (Th < Tl)
        std::swap(Th, Tl);

    cv::Mat bw_h = cv::Mat(Suppimg.size(), CV_8UC1, cv::Scalar(0));
    cv::Mat bw_l = cv::Mat(Suppimg.size(), CV_8UC1, cv::Scalar(0));

    for (int i = 0; i < Suppimg.rows; i++)
        for (int j = 0; j < Suppimg.cols; j++)
        {
            if (Suppimg.at<ushort>(i, j) >= Th)
                bw_h.at<uchar>(i, j) = 255;
            else
                bw_h.at<uchar>(i, j) = 0;

            if (Suppimg.at<ushort>(i, j) >= Tl and Suppimg.at<ushort>(i, j) < Th)
                bw_l.at<uchar>(i, j) = 255;
            else
                bw_l.at<uchar>(i, j) = 0;
        }

    Edgeimg = bw_h.clone();
    for (int i = 1; i < Suppimg.rows - 1; i++)
        for (int j = 1; j < Suppimg.cols - 1; j++)
            if (bw_h.at<uchar>(i, j) == 255)
            {
                if (bw_l.at<uchar>(i - 1, j - 1) == 255)
                    Edgeimg.at<uchar>(i - 1, j - 1) = 255;
                if (bw_l.at<uchar>(i - 1, j) == 255)
                    Edgeimg.at<uchar>(i - 1, j) = 255;
                if (bw_l.at<uchar>(i - 1, j + 1) == 255)
                    Edgeimg.at<uchar>(i - 1, j + 1) = 255;
                if (bw_l.at<uchar>(i, j - 1) == 255)
                    Edgeimg.at<uchar>(i, j - 1) = 255;
                if (bw_l.at<uchar>(i, j + 1) == 255)
                    Edgeimg.at<uchar>(i, j + 1) = 255;
                if (bw_l.at<uchar>(i + 1, j - 1) == 255)
                    Edgeimg.at<uchar>(i + 1, j - 1) = 255;
                if (bw_l.at<uchar>(i + 1, j) == 255)
                    Edgeimg.at<uchar>(i + 1, j) = 255;
                if (bw_l.at<uchar>(i + 1, j + 1) == 255)
                    Edgeimg.at<uchar>(i + 1, j + 1) = 255;
            }
}

Canny函数

手搓的Canny函数：

void Canny_Edge(cv::Mat input, cv::Mat &output, int th, int tl, int size, double sigma)
{
    cv::Mat Gaussimg, Gradimg, Direimg, Suppimg, Edgeimg;
    Gaussfilter(input, Gaussimg, size, sigma);
    GradDire(Gaussimg, Gradimg, Direimg);
    NonMaxSuppression(Gradimg, Direimg, Suppimg);
    doubleThread(Suppimg, Edgeimg, tl, th);
    output = Edgeimg;
}

OpenCV自带的Canny函数；

1	void Canny(InputArray image, OutputArray edges, double threshold1, double threshold2, int apertureSize = 3, bool L2gradient = false);

参数；

image：8比特输入图像。
edges：输出边缘图，单通道8位图像，与图像大小相同。
threshold1：滞后过程的第一个阈值。
threshold2：滞后过程的第二个阈值。
apertureSize：Sobel算子大小。
L2gradient：计算图像梯度复制的标识。

效果截图

int main()
{
    cv::Mat src = cv::imread("src/lena.jpg");
    cv::Mat dst1, dst2;
    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    Canny_Edge(src, dst1, 50, 20, 3, 1);
    cv::Canny(src, dst2, 50, 20, 3, 1);

    cv::namedWindow("手搓Canny", cv::WINDOW_NORMAL);
    cv::namedWindow("Canny函数", cv::WINDOW_NORMAL);
    cv::imshow("手搓Canny", dst1);
    cv::imshow("Canny函数", dst2);
    cv::waitKey(0);
    return 0;
}

11.2 图像阈值分割

图像分割都是基于图像像素的灰度值，通过一个阈值T将图像中的像素分为两类或多类。

阈值分割的基本原理：

g(x,y)=\begin{cases} 1,\quad if\ f(x,y)>T\\ 0, \quad if\ f(x,y)\leq T \end{cases}

一般的图像阈值分割方法都主要在于去通过图像自身信息去计算寻找合适的阈值。

11.2.1 全局阈值分割

迭代阈值分割

计算步骤：

为全局阈值T选择一个初始的估计值，一般是图像平均灰度值。
使用初始值T进行阈值分割，此时图像分为大于阈值的像素组G1和小于阈值的像素组G2；
分别计算属于G1、G2图像像素的平均灰度值m1和m2；
针对m1和m2计算一个新的阈值 $T=\frac{m1 + m2} {2}$ ；
重复2到4，直到连续迭代中计算的连续两个T的差小于某个预定义的值为止。

代码如下：

#include <opencv2/opencv.hpp>

void imageIterativeThresholdSegmentation(cv::Mat input, cv::Mat &output)
{
    cv::Mat src = input.clone();

    if (src.channels() == 3)    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);
    double T = 0, preT = 0;

    for (int i = 0; i < src.rows; i ++)
        for (int j = 0; j < src.cols; j ++)
            T += src.at<uchar>(i, j);

    T = 1.0 * T / (src.rows * src.cols);

    while (std::abs(preT - T) > 0.5)
    {
        preT = T;
        int mean1 = 0, mean2 = 0, cnt1 = 0, cnt2 = 0;
        for (int i = 0; i < src.rows; i ++)
            for (int j = 0; j < src.cols; j ++)
            {
                if (src.at<uchar>(i, j) > T)
                    mean1 += src.at<uchar>(i, j), cnt1 ++;
                else
                    mean2 += src.at<uchar>(i, j), cnt2 ++;
            }

        mean1 = 1.0 * mean1 / cnt1;
        mean2 = 1.0 * mean2 / cnt2;
        T = (mean1 + mean2) / 2;
    }

    cv::threshold(src, output, T, 255, cv::THRESH_BINARY);
}

int main()
{
    cv::Mat src = cv::imread("src/lena.jpg");
    cv::Mat dst1;
    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    imageIterativeThresholdSegmentation(src, dst1);

    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dst1", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    cv::imshow("dst1", dst1);

    cv::waitKey(0);
    return 0;
}

效果截图：

OTSU大津法阈值分割

计算步骤：

计算图像灰度直方图的零阶累积距（累加直方图）：

zeroCumuMoment(k)=\sum_{i=1}^khistogram(i),k\in[0,255]

计算灰度直方图的一阶累积距：

oneCumuMoment(k)=\sum_{i=1}^k(i*histogram(i)),k\in[0,255]

计算输入图像的总体灰度平均值mean，也就是k=255时的一阶累积距：

mean=oneCumuMoment(255)

计算每一个灰度级作为阈值时，前景区域的平均灰度、背景区域的平均灰度与整体图像平均灰度的方差，方差计算：

\sigma^2(k)=\frac{(mean*zeroCumuMoment(k)-oneCumuMoment(k))^2} {zeroCumuMoment(k)*(1-zeroCumuMoment(k))},k\in[0,255]

找到最大的 $\sigma^2(k)$ ，即是所求的阈值：

thresh=\max(\sigma^2(k)),k\in[0,255]

代码如下：

#include <opencv2/opencv.hpp>

void imageotsuThresholdSegmentation(cv::Mat input, cv::Mat &output)
{
    cv::Mat src = input.clone();

    if (src.channels() == 3)    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    // 计数灰度直方图各像素值
    int hist[256] = { 0 };
    for (int i = 0; i < src.rows; i ++)
        for (int j = 0; j < src.cols; j ++)
            hist[src.at<uchar>(i, j)] ++;

    // 计算灰度直方图各像素概率
    double phist[256] = { 0 };
    for (int i = 0; i < 256; i ++)
        phist[i] = 1.0 * hist[i] / (src.rows * src.cols);

    double zeroCumuMoment[256] = { 0 }, oneCumuMoment[256] = { 0 };

    // 计算灰度直方图的零阶累积距和一阶累积距
    zeroCumuMoment[0] = phist[0];
    oneCumuMoment[0] = 0 * phist[0];
    for (int i = 1; i < 256; i ++)
    {
        zeroCumuMoment[i] = zeroCumuMoment[i - 1] + phist[i];
        oneCumuMoment[i] = oneCumuMoment[i - 1] + i * phist[i];
    }

    double mean = oneCumuMoment[255];

    double _max = -1;
    int threshold = 0;

    for (int i = 0; i < 256; i ++)
    {
        double tmp = mean * zeroCumuMoment[i] - oneCumuMoment[i];
        double tmp1 = zeroCumuMoment[i] * (1 - zeroCumuMoment[i]);
        double ans = tmp * tmp / tmp1;
        if (_max < ans)
        {
            _max = ans;
            threshold = i;
        }
    }

    cv::threshold(src, output, threshold, 255, cv::THRESH_BINARY);
}

int main()
{
    cv::Mat src = cv::imread("src/lena.jpg");
    cv::Mat dst1;
    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    imageotsuThresholdSegmentation(src, dst1);

    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dst1", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    cv::imshow("dst1", dst1);

    cv::waitKey(0);
    return 0;
}

11.2.2 可变阈值处理

将图像划分为多个局部，对于每个局部都采取阈值分割，使得效果更好。

11.2.3 更多

使用超像素分割图像
使用图割分割区域
使用形态学分水岭分割区域

2024-01-07 该篇文章被 Fingsinz 打上标签: CPP OpenCV 图像处理归为分类: 笔记