关键词:C++、机器学习
基础概念
机器学习是研究如何在计算机上 从数据产生模型 的学问。
基本术语
数据:用于学习的输入内容,通常是一组或多组记录。
数据集:记录的集合。
学习、训练:从数据集中学习模型的过程,通过执行某个学习算法完成。
- 训练集:用于训练的数据集合。
- 测试集:用于通过模型预测结果的数据集合,评估模型优劣。
- 验证集:用于纠正和强化模型的数据集合
| 类别 |
验证集 |
测试集 |
| 是否参与训练 |
否 |
否 |
| 作用 |
多次使用,不断调整 |
仅仅在最终模型评估时使用 |
西瓜书(周志华的机器学习)中提到
一批关于西瓜的数据,如(色泽=青绿;根蒂=蜷缩;敲声=浊响)、(色泽=乌黑;根蒂=稍蜷;敲声=沉闷)……
其中每对括号内时一条记录,记录的集合为数据集。
- 每条记录是关于一个对象的描述,称为一个样品。
- 反映对象在某方面的表现或性质的事项,称为属性或特征。
- 属性的取值为属性值
- 属性所组成的空间称为属性空间、样本空间或输入空间。
- 可以根据色泽、根蒂、敲声的取值确定一个对象,由这三者可组成向量,称为特征向量。
通常,令 D={x1,x2,...,xm} 表示包含 m 个样本的数据集,每个样本又由 d 个属性描述,xi=(xi1,xi2,...,xid)。d 通常称为样本的维数,表示样本的属性个数。
通过学习得到模型,即可在没剖开一个西瓜之前,预测未知的西瓜。建立关系:
((色泽=青绿;根蒂=蜷缩;敲声=浊响),好瓜)
- 逗号前面是前面提过的特征向量。
- 逗号后面是结果,称为标签(标记)。
- 即 (xi,yi)
只预测是“好瓜”或者“坏瓜”的任务称为分类任务。
- 只涉及两个类别称为二分类,通常为正类和反类。
- 涉及多个类别称为多分类。
预测连续的值,如西瓜的成熟度,称为回归任务。
当事先不知道某些概念,通过学习发现将西瓜分成若干组(如“外地瓜”“本地瓜”),称为聚类任务。
又根据训练数据是否拥有标记信息,学习任务可以分为监督学习和无监督学习。
- 分类和回归是监督学习的代表
- 聚类是无监督学习的代表
泛化:模型适用于新样本的能力。
经验误差与过拟合
分类错误的样本数占样本总数的比例称为错误率。
错误率=ma,在m个样本中有a个样本分类错误精度=1−错误率=(1−ma)×100%
误差:模型的实际预测输出与样本的真实输出之间的差异。
- 训练集上的误差称为训练误差或经验误差
- 新样本上的误差称为泛化误差
过拟合:模型对训练集的某些特殊特点过于重视,泛化性能下降。
- 比如对西瓜数据集训练识别西瓜,西瓜大小被过于重视,认为小西瓜(或远处的西瓜)不是西瓜。
欠拟合:模型对训练样本的一般性质拟合不足。
- 比如对西瓜数据集训练识别西瓜,认为绿色的都是西瓜。
线性模型
基本形式
对于一个样本 x=(x1,x2,...,xd),其中 xi 为第 i 个属性上的取值。
线性模型试图通过一个属性值与权值的线性组合进行预测:
f(x)=ω1x1+ω2x2+...+ωdxd+b
向量模式写成:
f(x)=ωTx+bω=(ω1,ω2,...,ωd)
线性回归
一元线性回归
线性回归对于样本 (xi,yi) ,试图使:
f(xi)=ωxi+b近似于yi
通过均方误差评估 f(xi) 与 yi 之间的差别,试图让均方误差取最小值:
(w∗,b∗)=(w,b)argmini=1∑m(f(xi)−yi)2=(w,b)argmini=1∑m(yi−f(xi))2(w∗,b∗)=(w,b)argmini=1∑m(yi−wxi−b)2
- (ω∗,b∗) 为 ω 和 b 的解,此处 m 为样本数。
- argmin 表示右式取最小值时 ω 和 b 的值。
- 求均方误差也对应了求欧氏距离。
基于均方误差最小值来进行模型求解,称为最小二乘法。
- 线性回归中,最小二乘法就是试图找到一条直线,使得样本到直线上的欧式距离之和最小。
令:
E(w,b)=i=1∑m(yi−wxi−b)2
上式分别对 ω 和 b 求导:
∂ω∂E(ω,b)=2(ωi=1∑mxi2−i=1∑m(yi−b)xi),∂b∂E(ω,b)=2(mb−i=1∑m(yi−wxi))
使导数为0,得到:
ω=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−x) b=m1i=1∑m(yi−ωxi)
- x 为 x 的均值。
例子-一元线性回归
对于一个一元线性回归数据集进行回归计算,效果如下:

该例子相关的数据集以及代码已置于仓库:Gitee
多元线性回归
用梯度下降求解多元线性回归。
- 梯度下降法的基本思想可以类⽐为⼀个下⼭的过程。
- 最快的下山方式就是找到当前位置最陡峭的⽅向,然后沿着此方向向下⾛,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的⽅向,就能让函数值下降的最快。
- 反复求取梯度,最后就能到达局部的最⼩值。
在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率;
在多变量函数中,梯度是⼀个向量(向量有方向),梯度的方向就指出了函数在给定点的上升最快的方向。
梯度下降公式为:
xi+1=xi−α∂xi∂f(xi)
- α 称作学习率或者步长,意味着每一步走的距离。距离太大容易错过最低点,距离太小迟迟未到最低点。
如:
- 单变量函数梯度下降: f(x)=x2
- 微分为:f′(x)=2x
- 初始化起点为: x0=1,学习率取0.4
- 梯度下降迭代:
- x1=x0−0.4×2x0=1−0.4×2=0.2
- x2=x1−0.4×2x1=0.2−0.4×0.4=0.04
- x3=x2−0.4×2x2=0.04−0.4×0.08=0.008
- x4=x3−0.4×2x3=0.008−0.4×0.016=0.0016
- 多变量函数的梯度下降: f(x)=x12+x22
- 微分为:f′(x)=2x1+2x2
- 初始化起点为: x0=(1,3),学习率取0.1
- 梯度下降迭代:
- x1=x0−0.1×f′(x0)=(1,3)−0.1×(2,6)=(0.8,2.4)
- x2=x1−0.1×f′(x1)=(0.8,2.4)−0.1×(1.6,4.8)=(0.64,1.92)
- x3=x2−0.1×f′(x2)=(0.64,1.92)−0.1×(1.28,3.84)=(0.512,1.536)
- ……
- x100=(1.6296e−10,4.8889e−10)
引入损失函数,度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。线性回归中假设模型函数为: f(x1,...,xn)=w0+w1x1+w2x2+...+wnxn
- wi 为模型参数,b 为偏置。
- 简化:增加特征 x0=1,可以简化为:f(x0,...,xn)=∑i=0nwixi
在线性回归中,损失函数通常为样本输出和假设函数的差取平方(或者带系数)。比如对于 m 个样本 (xi,yi)(i=1,2,...m),采⽤线性回归,假设损失函数为:
Loss(w0,w1,...,wn)=2m1j=0∑m(f(x0(j),x1(j),...,xn(j))−yj)2
- xi(j):上标 j 表示第 j 个样本,下标 i 表示第 i 个特征。
- 系数 21 是方便微分化简。
- x0(j) 都为1。
对于上述损失函数的梯度为:
∂wi∂Loss(w0,w1,...,wn)=m1j=0∑m(f(x0(j),x1(j),...,xn(j))−yj)xi(j)
接着变化:
wi=wi−αm1j=0∑m(f(x0(j),x1(j),...,xn(j))−yj)xi(j)
梯度算法变种
- 全梯度下降算法(Full Gradient Descent)
wi=wi−αj=0∑m(f(x0(j),x1(j),...,xn(j))−yj)xi(j)
- 随机梯度下降算法(Stochastic Gradient Descent)
- 每次只代⼊计算⼀个样本⽬标函数的梯度来更新权重,再取下⼀个样本重复此过程,直到损失函数值停⽌下降或损失函数值⼩于某个可以容忍的阈值。
wi=wi−α(f(x0(j),x1(j),...,xn(j))−yj)xi(j)
- 小批量梯度下降算法(Mini-batch Gradient Descent)
- 每次从训练样本集上随机抽取⼀个⼩样本集,在抽出来的⼩样本集上采⽤FG迭代更新权重。
wi=wi−αj=t∑t+x−1(f(x0(j),x1(j),...,xn(j))−yj)xi(j)
- 随机平均梯度下降算法(Stochastic Average Gradient Descent)
- 在内存中为每⼀个样本都维护⼀个旧的梯度,随机选择第i个样本来更新此样本的梯度,其他样本的梯度保持不变,然后求得所有梯度的平均值,进⽽更新了参数。
- m 个样本
wi=wi−mα(f(x0(j),x1(j),...,xn(j))−yj)xi(j)
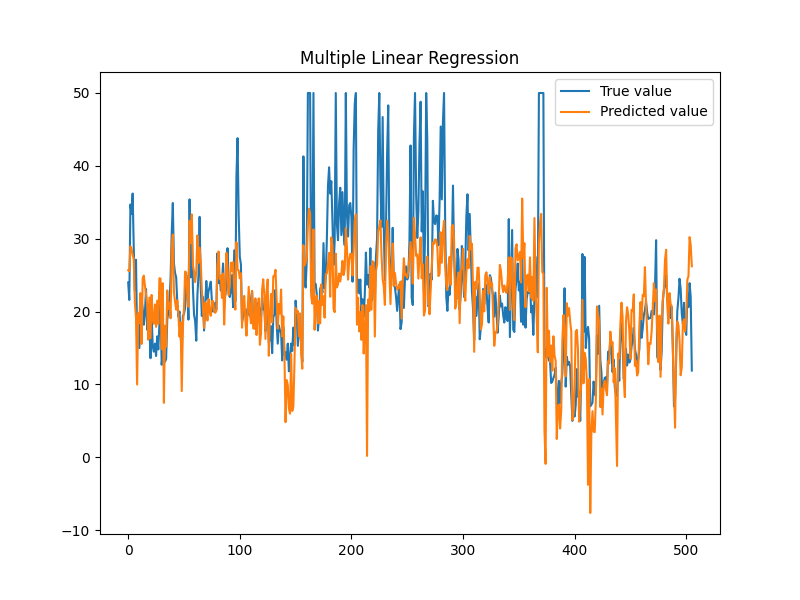
例子-波士顿房价
数据集地址:https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data
数据集具有14列:
- CRIM:城镇人均犯罪率。
- ZN:占地面积超过25,000平方英尺的住宅用地比例。
- INDUS:每个城镇非零售业务的比例。
- CHAS:Charles River虚拟变量(如果是河道,则为1;否则为0)。
- NOX:一氧化氮浓度(每千万份)。
- RM:每间住宅的平均房间数。
- AGE:1940年以前建造的自住单位比例。
- DIS:波士顿的五个就业中心加权距离。
- RAD:径向高速公路的可达性指数。
- TAX:每10,000美元的全额物业税率。
- PTRATIO:城镇的学生与教师比例。
- B:1000(Bk−0.63)2 其中Bk是城镇黑人的比例。
- LSTAT:人口状况下降%。
- MEDV:自有住房的中位数报价, 单位1000美元。
- 前13列为属性值(即 xi),第14列为房价(即 y)。
使用 SAG 算法进行线性回归计算。
测试结果:
1
2
3
| Data imported: 506
平均误差:4.57072
迭代时长:46.329s
|
该例子相关的数据集以及代码已置于仓库:Gitee
贝叶斯分类器
假设有 N 个类别,B={B1,B2,...,BN},现有样本 A,通过贝叶斯公式:
P(Bi∣A)=∑j=1nP(Bj)P(A∣Bj)P(Bi)P(A∣Bi)
- P(Bi):类别 Bi 发生的概率。
- 称作先验概率,表达了样本空间中各类样本所占的概率。
- 根据大数定律,当训练集包含充足的独立同分布样本时,P(Bi) 可通过各类样本出现的频率来进行估计
- P(A∣Bi):确定是 Bi 类下,样本 A 出现的概率。称作类条件概率。
- P(Bi∣A):在样本 A 出现下,属于类别 Bi 的概率。称作后验概率。
类条件概率通过数据集进行训练,估计参数 θb。
令 Di 表示训练集 D 中第 i 类样本组成的集合,假设样本是独立同分布,则参数 θb 对于数据集的似然是:
P(Di∣θb)=x∈Di∏P(x∣θb)
对 θb 进行极大似然估计,寻找最大化似然 P(Di∣θb) 的参数值 θb′。
- 从 θb 的所有可能取值中,找到一个能使数据出现可能性最大的值。
连乘容易出现下溢,可以使用对数计算:
LL(θb)=logP(Di∣θb)=x∈Di∑logP(x∣θb)
θb′=θbargmaxLL(θb)
朴素贝叶斯分类器
一种基于贝叶斯理论的简单概率分类器。
由属性条件独立性:
P(Bi∣A)=∑j=1nP(Bj)P(A∣Bj)P(Bi)P(A∣Bi)=P(A)P(Bi)i=1∏dP(A(i)∣Bi)
- d:样本的属性个数。
- Bi:第 i 个类别。
- A(i):样本 A 的第 i 个属性值。
- 对于所有类别, P(A) 都相等。
所以朴素贝叶斯表达式写成:
f(A)=Bi∈BargmaxP(Bi)j=1∏dP(A(j)∣Bi)
朴素贝叶斯的训练过程就是基于训练集 D 来估计类先验概率 P(Bi),并为每个属性估计条件概率 P(A(j)∣Bi)。
先验概率:
P(Bi)=∣D∣∣Di∣
离散属性下,设 DBi,A(j) 为第 Bi 类,第 j 个属性值为 A(j) 构成的集合,则条件概率可估计为:
P(A(j)∣Bi)=∣DBi∣∣DBi,A(j)∣
连续属性则考虑概率密度函数。
如果某个属性值在训练集中没有与某个类同时出现过,可能会出现概率值为零,此时需要做一些平滑。
P^(Bi)=∣D∣+N∣Di∣+1
P^(A(j)∣Bi)=∣DBi∣+Nj∣DBi,A(j)∣+1
- N:训练集中可能的类别数;
- Nj:第 j 个属性可能的取值数。
拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题,并且在训练集变大时,修正过程所引入的先验的影响也会逐渐变得可忽略,使得估值渐趋向于实际概率值。
正态贝叶斯分类器
正态贝叶斯分类器认为每一个分类的所有特征属性(即特征向量)服从多变量正态高斯分布,即:
P(x∣Ck)=(2π)n∣∑k∣1exp(−21(x−μk)Tk∑−1(x−μk))
- μk 表示第 k 个分类对应的 n 维均值向量;
- ∣∑k∣ 表示第 k 个分类对应的 n×n 的协方差矩阵 ∑k 的行列式的值。
正态贝叶斯分类器只能处理特征属性是连续数值的分类问题。但它认为特征属性直接不必独立,比朴素贝叶斯的使用条件宽。
同样,计算最大似然:
y^=k∈{1,...,k}argmaxP(x1,...,xn∣Ck)
化为对数似然函数:
ln(L)=−21[ln(∣k∑∣)+(x−μk)Tk∑−1(x−μk)+nln(2π)](1)
求式上极大值问题可以转换为求式中方括号内的极小值问题。
均值向量 μk 的第 i 个特征属性 μki 的极大似然估计为:
μ^ki=Nk∑j=1Nkxki(j)
- xki(j):训练样本中属于分类 k 的第 j 个样本的第 i 个特征属性的值。
- Nk:训练样本中属于分类 k 的样本数。
μk^=(μ^k1,...,μ^kn)T(2)
n×n 的协方差矩阵 ∑k 的无偏估计形式为:
∑^k=Nk−11⎣⎢⎢⎢⎢⎢⎡covk(1,1)covk(2,1)⋮covk(n,1)covk(1,2)covk(2,2)⋮covk(n,2)......⋱...covk(1,n)covk(2,n)⋮covk(n,n)⎦⎥⎥⎥⎥⎥⎤(3)
其中 covk(p,q) 表示训练样本中第 k 个分类所组成的数据集合中,第 p 个特征属性与第 q 个特征属性的协方差,如果 p=q,那么为方差。
covk(p,q)==∑j=1Nk[(xkp(j)−μ^kp)(xkq(j)−μ^kq)]∑j=1Nk(xkp(j)xkq(j))−μ^kq∑j=1Nkxkp(j)−μ^kp∑j=1Nkxkq(j)+Nkμ^kpμ^kq
正态贝叶斯分类器的执行步骤:
- 由训练样本数据估计每个分类的协方差矩阵(式3)和均值向量(式2);
- 把协方差矩阵和均值向量代入到对数似然函数(式1);
- 得到每个分类完整的对数似然函数;
- 预测样本时,将样本的特征属性分别代入全部分类的对数似然函数中,最大对数似然函数对应的分类就是该样本的分类结果。
基于OpenCV实现正态贝叶斯分类器
OpenCV 自带实现了 正态贝叶斯分类器 的类: NormalBayesClassifier。
相关代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
cv::Ptr<cv::ml::NormalBayesClassifier> model=cv::ml::NormalBayesClassifier::create();
cv::Ptr<cv::ml::TrainData> tData =cv::ml::TrainData::create(datas, ROW_SAMPLE, labels);
model->train(tData);
int label = model->predict(samples)
model->save(filename)
|
例子-糖尿病预测数据集
数据集地址:https://aistudio.baidu.com/datasetdetail/33810
- 该数据集包含数据集中共包含768个样本,取后100个数据组成测试集。
数据集中每个样本有8种特征。Outcome 是样本的标签(即类别),0表示没有糖尿病,1表示患有糖尿病。
- Pregnancies: 怀孕次数
- Glucose:血浆葡萄糖浓度
- BloodPressure:舒张压
- SkinThickness:肱三头肌皮肤褶皱厚度
- Insulin:两小时胰岛素含量
- BMI:身体质量指数,即体重除以身高的平方
- DiabetesPedigreeFunction:糖尿病血统指数,即家族遗传指数
- Age:年龄
使用手搓的朴素贝叶斯分类器和 OpenCV 实现的正态贝叶斯分类器进行训练测试,结果如下:
1
2
3
4
5
6
7
8
9
10
11
| Train Data imported: 668
正态贝叶斯分类器:
计算花费时长:0ms
Test Data imported: 100
正确率:0.76
Train Data imported: 668
朴素贝叶斯分类器:
计算花费时长:1ms
Test Data imported: 100
正确率:0.59
|
代码及数据集地址:Gitee - bayesClassifier
例子-鸢尾花数据集
数据集地址:
部分数据如下:
| 花萼长度 |
花萼宽度 |
花瓣长度 |
花瓣宽度 |
类别 |
| 6.4 |
2.8 |
5.6 |
2.2 |
2 |
| 5.0 |
2.3 |
3.3 |
1.0 |
1 |
| 4.9 |
2.5 |
4.5 |
1.7 |
2 |
| 4.9 |
3.1 |
1.5 |
0.1 |
0 |
使用手搓的朴素贝叶斯分类器和 OpenCV 实现的正态贝叶斯分类器进行训练测试,结果如下:
1
2
3
4
5
6
7
8
9
10
11
| Train Data imported: 120
正态贝叶斯分类器:
计算花费时长:0ms
Test Data imported: 30
正确率:0.966667
Train Data imported: 120
朴素贝叶斯分类器:
计算花费时长:0ms
Test Data imported: 30
正确率:0.8
|
代码及数据集地址:Gitee - bayesClassifier
初探 EM 算法
EM 介绍
期望极大值(Expectation Maximization,EM)算法是一种能够得到极大似然参数估计的迭代方法。
令 X 表示已观测变量集,Z 表示隐变量集,θ 表示模型参数,如果想对 θ 作极大似然估计,则最大化对数似然应为:
LL(θ∣X,Z)=lnP(X,Z∣θ)
由于 Z 是隐变量,故无法直接求解。可以通过对 Z 计算期望,来最大化已观测数据的对数“边际似然”:
LL(θ∣X)=lnP(X∣θ)=lnZ∑P(X,Z∣θ)(1)
EM 算法的基本思想:
- E-step:若参数 θ 已知,则根据训练数据推断除最优隐变量 Z 的值。
- M-step:若隐变量 Z 的值已知,则对参数 θ 作极大似然估。
若计算 Z 的期望,以 θ0 为起点,对式1迭代以下步骤直至收敛:
- E-step:基于 θt 推断隐变量 Z 的期望,记作 Zt;
- M-step:基于已观测变量 X 和 Zt 对参数 θ 作极大似然估计,记作 θt+1。
若基于 θt 计算隐变量 Z 的概率分布 P(Z∣X,θt),则 EM 的步骤变成:
- E-step:基于 θt 推断隐变量分布 P(Z∣X,θt),并计算对数似然 LL(θ∣X,z) 关于 Z 的期望:
Q(θ∣θt)=EZ∣X,θtLL(θ∣X,Z)
θi+1=θargmaxQ(θ∣θt)
基于OpenCV实现EM
EM 是一种无监督的机器学习方法,它还可以用于聚类处理上。
OpenCV 提供了 EM 类,可用于实现 EM 算法对高斯混合模型的参数估计:
- 高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型,这 K 个子模型是混合模型的隐变量。
1
2
3
4
5
6
7
8
|
cv::Ptr<cv::ml::EM> model=cv::ml::EM::create();
model->setClustersNumber(classes);
bool trainEM(InputArray samples,OutputArray logLikelihoods=noArray(),OutputArray labels=noArray(),OutputArray probs=noArray()) ;
|
使用 EM 算法进行像素聚类进而实现图像分割。
- 将 RGB 属性作为样本,进行聚类。即每一个像素都是一个样本。
效果如下:

代码地址:EM 算法 - Gitee
K 近邻(KNN)算法
K 近邻算法(K-Nearest Neighbors,KNN)既可以处理分类问题,也可以处理回归问题。
KNN 是一种懒惰学习算法。
- 懒惰学习算法:指直到出现新的测试样本,该算法才开始依据训练样本进行样本的预测处理工作。
- 也就是说,该算法事先不会对训练样本进行任何处理,只会懒散地等待测试样本的到来,然后才开始工作。
懒惰学习算法构建的目标函数能够更近似测试样本数据本身,但同时它需要更大的存储空间用于存储训练样本数据。
- 懒惰学习算法非常适用于 具有较少特征属性 的 大型数据库 的问题。
KNN 算法原理
在训练集中,每个样本假设都是一个具有 n 个特征属性的向量,即 x=(x1,x2,x3,...,xn) ,可看作每个样本在 n 维特征空间内分布。每个样本还有一个标签 y。
目的是找到一个函数,使得 y=f(x),以确定新样本 u 的标签。
样本在 n 维特征空间内分布,可以找到样本间的一种“距离”,用于评估样本间的相似程度。
DEu(x,u)=i=1∑n(xi−ui)2
DMan(x,u)=i=1∑n∣xi−ui∣
DMin=qi=1∑n∣xi−ui∣q
DHam(x,u)=i=1∑n∣xi−ui∣,{当xi=ui时,DHam(x,u)=0当xi=ui时,DHam(x,u)=1
KNN 的任务是在训练集中,依据距离找到与新样本(测试样本) u 最相似的那 K 个训练样本。
- 若做分类问题,则多数表决,在 K 个训练样本中,哪个分类的样本数多,哪个分类就是 u 的预测分类。
- 若做回归问题,u 的预测值 v 为:
v=K∑i=1Kyi
在考虑训练集与测试样本之间距离大小的影响下,使得距离更小的样本具有更大的权值,K 个最邻近样本中第 i 个样本 xi 与测试样本 u 的权值定义为:
w(xi,u)=∑i=1nexp(−D(xi,u))exp(−D(xi,u))
v=i=1∑Kw(xi,u)yi
KNN 的 K 需要预先确定:
- 若值过大,会使特征空间内明确分类边界变得模糊;
- 若值过小,则引入误差。
常用 交叉验证法 选择 K 值。
- 把训练数据 D 分为 K 份,用其中的 (K−1) 份训练模型,把剩余的1份数据用于评估模型的质量。
基于OpenCV实现KNN
OpenCV 并没有采用交叉验证和距离权值的方法。
相关函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
cv::Ptr<cv::ml::KNearest> model=cv::ml::KNearest::create();
model->setDefaultK(k);
model->setIsClassifier(true);
model->setAlgorithmType(cv::ml::KNearest::BRUTE_FORCE);
model->train(trainDataPtr);
model->findNearest(testMat, k, result);
|
例子-小麦品种籽粒数据集
数据集地址:https://archive.ics.uci.edu/dataset/236/seeds
三种不同小麦品种籽粒几何特性的测定。数据集具有7个属性:
- 一个区域
- 周边P
- 紧性 C=4×π×A/P2
- 核的长度
- 核的宽度
- 不对称系数
- 核槽长度
部分数据如下:
| area |
perimeter |
compactness |
length of kernel |
width of kernel |
asymmetry coefficient |
length of kernel groove |
class |
| 15.26 |
14.84 |
0.871 |
5.763 |
3.312 |
2.221 |
5.22 |
1 |
| 14.88 |
14.57 |
0.8811 |
5.554 |
3.333 |
1.018 |
4.956 |
1 |
| 14.29 |
14.09 |
0.905 |
5.291 |
3.337 |
2.699 |
4.825 |
1 |
| 13.84 |
13.94 |
0.8955 |
5.324 |
3.379 |
2.259 |
4.805 |
1 |
| 16.14 |
14.99 |
0.9034 |
5.658 |
3.562 |
1.355 |
5.175 |
1 |
| 14.38 |
14.21 |
0.8951 |
5.386 |
3.312 |
2.462 |
4.956 |
1 |
| 12.74 |
13.67 |
0.8564 |
5.395 |
2.956 |
2.504 |
4.869 |
1 |
使用自实现 KNN 和 OpenCV 提供的 KNN 类进行训练计算,结果如下:
1
2
3
4
5
6
7
8
9
10
11
| Train Data imported: 150
Test Data imported: 60
K近邻算法:
正确率:0.933333
计算花费时长:1ms
Train Data imported: 150
Test Data imported: 60
K近邻算法(基于OpenCV实现):
正确率:0.95
计算花费时长:50ms
|
代码及数据集地址:KNN - Gitee
SVM 支持向量机算法
- SVM(Support Vector Machine):支持向量机
- SVC(Support Vector Classifier):支持向量分类器
- SVR(Support Vector Regression):支持向量回归器
支持向量机基本型
给定大小为 m 的训练集 D={(x1,y1),(x2,y2),…,(xm,ym)},yi∈{−1,1}。基于训练集 D 在样本空间中找到一个超平面,将不同类别的样本分开,如下图:

明显红色的划分超平面更合适。划分超平面可通过线性方程描述:
wTx+b=0
- w=(w1,w2,…,wn):为法向量,决定了超平面的方向;
- b:位移项。
- x=(x1,x2,…,xn)
样本空间中任意点到超平面 (w,b) 的距离为:
r=∣∣w∣∣∣wTx+b∣
在做分类时,应有 (xi,yi)∈D,当 yi=+1 时,wTxi+b>0;当 yi=−1 时,wTxi+b<0。令:
{wTxi+b≥+1,yi=+1wTxi+b≤−1,yi=−1
距离超平面最近的几个训练样本点满足上式,如下图 H1、H2 上的样本被称为支持向量(support vector)。
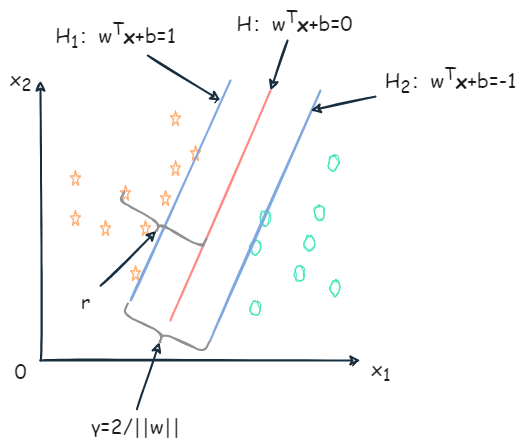
两个异类的支持向量到超平面的距离之和(也称为间隔)为:
γ=∣∣w∣∣∣(b+1)−(b−1)∣=∣∣w∣∣2
为了找到具有最大间隔的划分超平面,需要满足下式中约束参数 w 和b,使得 γ 最大:
w,bmax∣∣w∣∣2同时保证 yi(wTxi+b)≥1,i=1,2,…,m.
为了最大化间隔,需要最大化 ∣∣w∣∣−1,等价于最小化 ∣∣w∣∣2
w,bmin21∣∣w∣∣2同时保证 yi(wTxi+b)≥1,i=1,2,…,m.
对上式使用拉格朗日乘子法可得到它的对偶问题。
-
拉格朗日乘⼦法是⼀种寻找多元函数在⼀组约束下的极值的方法。
- 通过引⼊拉格朗日乘子,可将有 d 个变量与 k 个约束条件的最优化问题转化为具有 d+k 个变量的⽆约束优化问题求解。
-
对上式每条约束添加拉格朗日乘子 αi≥0
-
对偶问题是原始问题的一种变换形式,它在数学上与原始问题密切相关,但可能具有不同的结构和性质。
L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))
- 其中 α=(α1,α2,…,αm)
令 L(w,b,α) 对 w 和 b 的偏导为零,可得
∂w∂L(w,b,α)=w−i=1∑mαiyixi=0⇒w=i=1∑mαiyixi
∂b∂L(w,b,α)=−i=1∑mαiyi=0⇒0=i=1∑mαiyi
将 w=∑i=1mαiyixi 代入 L(w,b,α),将 w 和 b 消去,再结合 0=∑i=1mαiyi,得到 minw,b21∣∣w∣∣2 的对偶问题:
αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj(1)
同时保证 i=1∑mαiyi=0,αi≥0,i=1,2,…,m.
求解出 α 后:
f(x)=wTx+b=i=1∑mαiyixiTx+b(2)
上述过程需满足 KKT 条件,即:
⎩⎪⎪⎨⎪⎪⎧αi≥0yif(x)−1≥0αi(yif(x)−1)=0
对任意训练样本 (xi,yi),总有 αi=0 或 yif(xi)=1。
- 若 αi=0,该样本不会出现在式 1 的求和中,也不会对 f(xi) 产生影响。
- 若 αi>0,则必有 yif(xi)=1,对应的样本点位于最大间隔边界上,即支持向量。
训练完后,大部分训练样本也不需要保留,最终模型仅与支持向量有关。
SMO
对于式 1 的求解,可以使用二次规划算法求解,也可以通过 SMO(Sequential Minimal Optimization) 算法求解。
SMO 的基本思路:
核函数
上述讨论训练样本是线性可分的(即存在划分超平面能正确分类),如果原始样本空间内不能存在这样的划分超平面,那么需要 将样本从原始空间映射到更高维的空间,使其在这个特征空间内线性可分。
- 令 ϕ(x) 表示将 x 映射后的特征向量,则在特征空间中划分超平面所对应的模型表示为:
f(x)=wTϕ(x)+b
其中 w 和 b 为模型参数,有:
w,bmin21∣∣w∣∣2同时保证 yi(wTϕ(xi)+b)≥1, i=1,2,…,m
其对偶问题是:
αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xi)Tϕ(xj)同时保证 i=1∑mαiyi=0,αi≥0,i=1,2,…,m
设计核函数:
κ(xi,xj)=<ϕ(xi),ϕ(xj)>=ϕ(xi)Tϕ(xj)
- 即 xi 与 xj 在特征空间的内积等于它们在原始样本空间通过函数 κ(⋅,⋅) 计算的结果。
所以之前的式子改写为:
αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjκ(xi,xj)同时保证 i=1∑mαiyi=0,αi≥0,i=1,2,…,m
求解后可得到:
f(x)=wTϕ(x)+b=i=1∑mαiyiϕ(xi)Tϕ(x)+b=i=1∑mαiyiκ(xi,x)+b
- 上式说明模型最优解可通过训练样本的核函数展开,展式称为支持向量展式。
定理:令 χ 为输入空间,κ(⋅,⋅) 式定义在 χ×χ 上的对称函数,则 κ 式核函数 当且仅当 对于任意数据 D={x1,x2,…,xm},核矩阵 K 总是半正定的:
K=⎣⎢⎢⎢⎢⎢⎢⎢⎡κ(x1,x1)⋮κ(xi,x1)⋮κ(xm,x1)⋯⋱⋯⋱⋯κ(x1,xj)⋮κ(xi,xj)⋮κ(xm,xj)⋯⋱⋯⋱⋯κ(x1,xm)⋮κ(xi,xm)⋮κ(xm,xm)⎦⎥⎥⎥⎥⎥⎥⎥⎤
- 对于一个半正定和矩阵,总能找到一个与之对应的映射 ϕ。任何一个核函数都隐式定义了一个称为“再生核希尔伯特空间”(简称RKHS)的特征空间。
常用核函数如下:
- 线性核:κ(xi,xj)=xiTxj;
- 多项式核:κ(xi,xj)=(xiTxj)d,d≥1 为多项式的次数;
- 高斯核:κ(xi,xj)=exp(−2σ2∣∣xi−xj∣∣2),σ>0 为高斯核的带宽;
- 拉普拉斯核:κ(xi,xj)=exp(−σ2∣∣xi−xj∣∣2),σ>0;
- Sigmoid核:κ(xi,xj)=tanh(βxiTxj+θ),tanh 为双曲正切函数,β>0,θ<0。
此外,核函数还可通过组合得到:
- 若 κ1 和 κ2 为核函数,则对于任意正数 γ1、γ2,其线性组合 γ1κ1+γ2κ2 也是核函数。
- 若 κ1 和 κ2 为核函数,则核函数的直积 κ1⊗κ2(xi,z)=κ1(xi,z)κ2(xi,z) 也是核函数。
- 若 κ1 为核函数,则对于任意函数 g(x),κ(x,z)=g(x)κ1(x,z)g(z) 也是核函数。
C-SVC算法
C-SVC算法:受参数 C 的制约。
- 参数 C 是最小的训练误差和最大的分类间隔的折中。
- 常用交叉验证法选取 C。
给定大小为 m 的训练集 D,其中每个样本具有 n 个属性,对应一个标签 yi∈{+1,−1} 表示其分类。
超平面方程表示为:
wTx+b=0
对每一个样本 xi,引入一个松弛变量 ξ≥0,作为错误分类误差的度量,可以被认为是在分类错误的情况下样本与属于它的间隔边界超平面的距离。
ξi={0,1−yi(wTxi+b),如果 yi(wTxi+b)≥+1如果 yi(wTxi+b)≤+1
由上式得到原公式下实现软间隔最大化的约束条件:
yi(wTxi+b)≥1−ξi, ξi≥0, i=1,2,…,m
如下图 H1 和 H2 之间的间隔称为软间隔:

在软间隔最大化中,被软间隔分隔错误的样本应该受到惩罚,且随着 ξi 增大而增加。还要尽可能减少错误分隔的样本数。软间隔最大化原公式如下:
min21∣∣w∣∣2+Ci=1∑mξi同时保证 yi(wTxi+b)≥1−ξi, ξi≥0,i=1,2,…,m
- C 为非负的惩罚参数,用于对分类错误样本的一定程度上的惩罚。
- C 大,相当于错误惩罚力度大。达到一定程度从而没有错误分类的样本,软间隔最大化等价于硬间隔最大化。
- C 小,相当于错误惩罚力度小。可能有更多样本被软间隔分类错误。
- ∑i=1mξi 为分类错误的总量。
对其进行构造拉格朗日方程:
L(w,b,α,ξ,μ)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))+i=1∑m(C−αi−μi)ξi
也求偏导得到
∂w∂L(w,b,α,ξ,μ)=w−i=1∑mαiyixi=0⇒w=i=1∑mαiyixi
∂b∂L(w,b,α,ξ,μ)=−i=1∑mαiyi=0⇒0=i=1∑mαiyi
∂ξi∂L(w,b,α,ξ,μ)=C−αi−μi=0
最后通过偏导式、拉格朗日方程、原公式得到软间隔对偶优化问题:
αmax−21i=1∑mj=1∑mαiαjyiyjxiTxj+i=1∑mαi同时保证 i=1∑mαiyi=0和0≤αi≤C, i=1,2,…,m
KTT 条件:
αi(yi(wTxi+b)−1+ξi)=0, (C−αi)ξi=0, i=1,2,…,m
- ξi=0, αi=0:样本被正确分类,并且这些样本不是支持向量,不影响最终解。
- ξi=0, 0<αi<C:样本在间隔超平面上,即这些向量是支持向量。
- 0<ξi≤1, αi=C:表示样本被分割超平面正确分类,但落在软间隔内。
- ξi>1, αi=C:样本被错误分类。
设 α∗=(α1∗,α2∗,…,αm∗) 为解,得到分隔超平面的法向量 w∗ 为:
w∗=i=1∑mαi∗yixi
然后通过 αi(yi(wTxi+b)−1+ξi)=0, (C−αi)ξi=0, i=1,2,…,m 计算 b,并把它的平均值作为分隔超平面的偏移量 b∗,则最终的决策函数为:
f(x)=sgn(i=1∑mαi∗yiK(xi⋅x)+b∗)
ν-SVC 算法
使用参数 ν 代替参数 C。
- 表示支持向量占全部训练样本的比例下限;
- 也表示错误分类样本占全部训练样本的比例上限。
- 如 ν=0.05,则保证最多有5%的训练样本被错分类,且至少有5%的支持向量。
用常系数 ν 代替参数 C,同时还引入一个需要被优化的变量 ρ,ν-SVC 的原公式:
min21∣∣w∣∣2−νρ+m1i=1∑mξi同时保证 yi(wTxi+b)≥ρ−ξi和ξi≥0,ρ≥0,i=1,2,…,m
ν-SVC 的软间隔宽度为:2ρ/∣∣w∣∣。
拉格朗日方程:
L(w,b,α,ξ,μ,ρ,δ)=21∣∣w∣∣2−νρ+m1i=1∑mξi−i=1∑mα[yi(wTxi+b)−ρ+ξi]−i=1∑mμξi−δρ
再次求偏导,使导数为0,得到:
w=i=1∑mαiyixi
αi+μi=m1
i=1∑mαiyi=0
i=1∑mαi−δ=0
结合,最终得到二次优化问题:
αmax−21i=1∑mj=1∑mαiαjyiyjK(xi,xj)同时保证 i=1∑mαiyi=0,0≤αi≤m1和i=1∑mαi≥ν, i=1,2,…,m
常系数 ν 仍需满足:
ν≤m2min(Nums(yi=+1),Nums(yi=−1))
- Nums(yi=+1) 表示样本中正例数量。
- Nums(yi=−1) 表示样本中负例数量。
决策函数为:
f(x)=sgn(i=1∑mαi∗yiK(xi,x)+b∗)
w=i=1∑mαiyixi
设两个集合 S+ 和 S−,集合内分别为正例和负例的支持向量(ξi=0),元素数量都为 s。约束变成 yif(xi)=ρ。得到 b∗ 和 ρ∗:
b∗=−2s1x∈S+∪S−∑i=1∑mαi∗yiK(x,xi)
ρ∗=2s1⎝⎜⎛x∈S+∑i=1∑mαi∗yiK(x,xi)−x∈S−∑i=1∑mαi∗yiK(x,xi)⎠⎟⎞
多类问题的 SVC
处理多类问题时,把多个类转化为若干个问题处理。
一对其余:用一类与其余类进行比较。
- 如将类1作为正例,其他组合一起作为负例,得到决策函数 f1(x);然后将类2作为正例,其余组合一起作为负例,得到决策函数 f2(x)。以此类推得到 k 个决策函数。
- 当对新样本 x,带入下式得到分类:
iargmaxfi(x)
一对一:一共得到 k(k−1)/2 个决策函数 fi,j(x),0≤i<j≤k,表示第 i 类和第 j 类比较得到的决策函数。
- 当对新样本 x,需要代入所有的 fi,j(x),统计所有类别的胜出次数,得票最多的类即为结果。
单类 SVM
单类问题并不是进行分类,而是判断新样本是否属于该类。
如判断银行业务中是否为欺诈交易时,无法提供足够多的欺诈例子用于训练,但有大量正常交易用于建模。
解决方法:Tax & Duin 法和 Schölkopf 法。
Tax & Duin 法:在输入空间或特征空间内找到一个体积最小的超球体,能够包含全部训练样本。
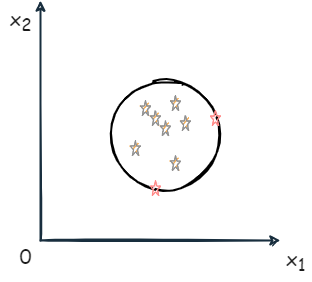
- 当然也为每个样本 xi 分配一个松弛变量 ξi
带有 ξi、球心为 a、半径为 R 的超球体表达式为:
F(R,a,ξi)=R2+Ci=1∑mξi
- C 是常数,用于平衡超球体的体积大小和超球体外样本的数量。
使得上式最小化,还需满足约束:
∣∣ϕ(xi)−a∣∣2≤R2+ξi,ξi≥0,i=1,2,…,m
- ϕ(xi) 表示样本 xi 从输入空间到特征空间的映射。
拉格朗日乘子法得到:
L(R,a,α,ξ,μ)=R2+Ci=1∑mξi−i=1∑mαi[R2+ξi−∣∣ϕ(xi)−a∣∣2]−i=1∑mμiξi
- αi 和 μi 都不小于0。
基于变量 R、a、ξi 的偏导数分别为:
i=1∑mαi=1
a=i=1∑mαiϕ(xi)
C−αi−μi=0
通过代入得到对偶公式:
L(R,a,α,ξ,μ)=i=1∑mαiϕ(xi)⋅ϕ(xi)−i=1∑mj=1∑mαiαjϕ(xi)⋅ϕ(xj)
使用核函数代替点乘,得到二次优化问题:
αmaxi=1∑mαiK(xi,xi)−i=1∑mj=1∑mαiαjK(xi,xj)受限于i=1∑mαi=1, 0≤αi≤C,i=1,2,…,m
在超球体表面的样本为支持向量。
- 超球体的半径 R 可通过计算球心 a 到任意一个支持向量的距离得到。
设解为 α∗=(α1∗,α2∗,⋯+αm∗),支持向量为 xs :
R2=∣∣ϕ(xj)−a∣∣∣2=∣∣ϕ(xs)−i=1∑mαi∗ϕ(xi)2∣∣=K(xs,xs)−2i=1∑mαi∗K(xs,xs)+i=1∑mj=1∑mαi∗αj∗K(xi,xj)
当判断样本是否属于该类时,需要计算样本 x 与球心的距离 a,并与半径 R 比较,如果小于半径,则是该类,否则不属于该类。
决策函数:
f(x)=sgn(d(x))
f(x)=sgn(R2−K(x,x)+2i=1∑mαi∗K(xi,x)−i=1∑mj=1∑mαi∗αj∗K(xi,xj))=sgn(K(xs,xs)−K(x,x)−2i=1∑mαi∗[K(xi,xs)−K(xi,x)])
- xs 表示任意一个支持向量;
- 当 f(x)=1,表示 x 属于该类。
Schölkopf 法:在特征空间找到一个超平面,该超平面能够分隔全部样本和坐标原点,并且要使该超平面到远点的距离最远。

求解:
min21∣∣w∣∣2+νm1i=1∑mξi−ρ受限于 (w⋅ϕ(xi))≥ρ−ξi,ξi≥0,i=1,2,…,m
- ν 表示支持向量占全部训练样本的比例下限,也表示错误分类样本占全部训练样本的比例上限。
做拉格朗日方程:
L(w,ξ,ρ,α,μ)=21∣∣w∣∣2+νm1i=1∑mξi−ρ−i=1∑mαi(w⋅ϕ(xi)−ρ+ξi)−i=1∑mμiξi
对 w、ξ、ρ 求偏导,使其为0,有:
w=i=1∑mαiϕ(xi)
αi=νm1−μi⇒αi≤νm1
i=1∑mαi=1
则对偶问题为:
αmax−21i=1∑mj=1∑mαiαiK(xi,xj)受限于 i=1∑mαi=1,0≤αi≤νm1,i=1,2,…,m
设解为 α∗=(α1∗,α2∗,⋯,αm∗),若 αi 和 μi 都不为0,则 ξi 必为0:
ρ=(w⋅ϕ(xs))
- xs 为任意一个支持向量。
由 αj 不为0,代入 w=∑i=1mαiϕ(xi),则:
ρ=(w⋅ϕ(xs))=i=1∑mαiK(xi,xs)
决策函数:
f(x)=sgn(d(x))=sgn((w⋅ϕ(x))−ρ)
f(x)=sgn(i=1∑mαi∗K(xi,x)−i=1∑mαi∗K(xi,xs))
- xs 为任意一个支持向量。
- x 为待预测样本。
- 当 f(x)=1,表示 x 属于该类。
ε-SVR 算法
Vapnik 通过 ε 不敏感损失函数,把 SVM 扩展到回归问题中。
设 yi 为样本 x 对应的响应值,回归问题则是找到一个函数 f(x),使得 f(xi)=yi。
Lossε={0,∣y−f(x)∣−ε,如果∣y−f(x)≤ε其他
- ε>0,表示控制误差限度的常量,即如果误差在 [−ε,ε] 之间,就认为忽略误差。
线性关系时,函数表示为:
f(x)=w⋅x+b

由于误差允许,所以在 f(x) 周围形成一个包围,称之为 ε 管。
ε-SVR 中,得到 f(x) 还需要满足:
- 使 f(x) 与测量值 yi 的偏差值不大于 ε,让所有样本都在 ε 管中。
- 使 f(x) 尽可能平坦,简化模型,能够避免过拟合。平直指的是样本中各个特征属性对样本贡献大小应该均衡,即 w 要小。
ε-SVR 问题表示为:
min21∣∣w∣∣2受限于{yi−w⋅xi−b≤εw⋅xi+b−yi≤ε,i=1,2,…,m
也使用软间隔,引入两个松弛变量 ξ+ 和 ξ−,上式改写为:
- ξi+ 表示那些被高估的样本响应值的误差;
- ξi− 表示那些被低估的样本响应值的误差
min21∣∣w∣∣2+Ci=1∑m(ξi++ξi−)受限于{yi−w⋅xi−b≤ε+ξi−w⋅xi+b−yi≤ε+ξi+, {ξi−≥0ξi+≥0, i=1,2,…,m
- C>0:为常数,均衡 f(x) 的平坦程度与偏差大于 ε 的样本数量。
∣ξ∣ε={0,∣ξ∣−ε,如果∣ξ∣≤ε其他
表示改写后的拉格朗日乘子法方程为:
L(w,b,ξ,α,μ)=21∣∣w∣∣2+Ci=1∑m(ξi++ξi−)−i=1∑m(μi+ξi++μi−ξi−)−i=1∑mαi+(ε+ξi++yi−w⋅xi−b)−i=1∑mαi−(ε+ξi−−yi+w⋅xi+b)
- αi+、αi−、μi+、μi− 都为非负值。
对原变量 w、b、ξ 进行求偏导并使其为0:
∂w∂L=w−i=1∑m(αi−−αi+)xi=0⇒w=i=1∑m(αi−−αi+)xi
∂b∂L=i=1∑m(αi+−αi−)=0
∂ξ+∂L=C−μi+−αi+=0
∂ξ−∂L=C−μi−−αi−=0
进入代入,得到对偶优化问题:
α−,α+max−21i=1∑mj=1∑m(αi−−αi+)(αj−−αj+)K(xi,xj)−εi=1∑m(αi−+αi+)+i=1∑myi(αi−−αi+)受限于 i=1∑m(αi−−αi+)=0, αi−,αj+∈[0,C]
- K(xi,xj):为核函数,同前映射关系。
设解为 α∗=(α1−∗,α1+∗,⋯,αm−∗,αm+∗),则:
w=i=1∑m(αi−∗−αi+∗)ϕ(xi)
最后回归计算公式:
f(x)=i=1∑m(αi−∗−αi+∗)K(xi,x)+b∗
由 KKT 条件计算:
b∗=yj−i=1∑m(αi−∗−αi+∗)K(xi,xj)+ε
或
b∗=yk−i=1∑m(αi−∗−αi+∗)K(xi,xk)−ε
- (xj,yj) 为任意一个样本对应的 αj+∗∈(0,C);
- (xk,yk) 为任意一个样本对应的 αk−∗∈(0,C)。
由 KKT 条件,还可以知道 αi−∗ 或 αi+∗ 等于 C 的样本在 ε 管外,而且 αi−∗ 或 αi+∗ 不可能同时为0。
这意味着一个样本不能拥有两个方向的松弛变量 ξ,只能向一个方向偏离。
ν-SVR 算法
Schölkopf 从 ν-SVC 算法上扩展得到 ν-SVR 算法。
ν-SVR 原公式:
min21∣∣w∣∣2+C(νε+m1i=1∑m(ξi++ξi−))受限于 {yi−w⋅ϕ(xi)−b≤ε+ξi−w⋅ϕ(xi)+b−yi≤ε+ξi+, {ξi−≥0ξi+≥0, i=1,2,…,m
ε-SVR 中,参数 ε 通过经验选取,而在 ν-SVR 中把 ε 作为目标函数的一个变量。同时 C 和 ν 为常数, C 为正值; ν∈[0,1] 同样表示支持向量占全部训练样本的比例下限,也表示错误估计样本占全部训练样本的比例上限。
取拉格朗日方程为:
L(w,b,β,ε,ξ,α,μ)=21+Cνε+mCi=1∑m(ξi++ξi−)−βε−i=1∑m(μi+ξi++μi−ξi−)−i=1∑mαi+(ε+ξi++yi−w⋅ϕ(xi)−b)−i=1∑mαi−(ε+ξi−−yi+w⋅ϕ(xi)+b)
对原变量 w、ε、b、ξ 求偏导并使之为0:
∂w∂L=w−i=1∑m(αi−−αi+)ϕ(xi)=0⇒w=i=1∑m(αi−−αi+)ϕ(xi)
∂ε∂L=Cν−i=1∑m(αi++αi−)−β=0
∂b∂L=i=1∑m(αi+−αi−)=0
∂ξ+∂L=mC−μi+−αi+=0
∂ξ−∂L=mC−μi−−αi−=−β
进入代入,得到对偶优化问题:
α−,α+max−21i=1∑mj=1∑m(αi−−αi+)(αj−−αj+)K(xi,xj)+i=1∑myi(αi−−αi+)受限于 i=1∑m(αi−−αi+)=0, αi−,αj+∈[0,mC], i=1∑m(αi++αi−)≤Cν
设解为 α∗=(α1−∗,α1+∗,⋯,αm−∗,αm+∗),则最后回归计算公式:
f(x)=i=1∑m(αi−∗−αi+∗)K(xi,x)+b∗
由 KKT 条件得到:
b∗=21[yi+yk−i=1∑m(αi−∗−αi+∗)K(xi,xj)−i=1∑m(αi−∗−αi+∗)K(xi,xk)]
- (xj,yj) 为任意一个样本对应的 αj+∗∈(0,C/N);
- (xk,yk) 为任意一个样本对应的 αk−∗∈(0,C/N)
解 ε∗ 为:
ε∗=i=1∑m(αi−−αi+)K(xi,xj)−yj+b∗
或
ε∗=yk−i=1∑m(αi−−αi+)K(xi,xj)−b∗
- (xj,yj) 为任意一个样本对应的 αj+∗∈(0,C/N);
- (xk,yk) 为任意一个样本对应的 αk−∗∈(0,C/N)
OpenCV所支持的 SVM
OpenCV 提供了五种支持向量机的类型,分别为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| enum Types {
C_SVC=100,
NU_SVC=101,
ONE_CLASS=102,
EPS_SVR=103,
NU_SVR=104
};
|
通过 SVM::setType(int val) 设置 SVM 类型,默认为 C_SVC。通过 SVM::getType() 获取 SVM 类型。
各个类型的 SVM 的超参可以通过以下函数访问:
- C:通过
SVM::setC(double val) 和 SVM::getC() 访问。
- ν:通过
SVM::setNu(double val) 和 SVM::getNu() 访问。
- ε:通过
SVM::setP(double val) 和 SVM::getP() 访问。
同时支持的核函数有:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| enum KernelTypes {
CUSTOM=-1,
LINEAR=0,
POLY=1,
RBF=2,
SIGMOID=3,
CHI2=4,
INTER=5
};
|
使用 SVM::setKernelType(int kernelType) 设置核函数类型。
- 多项式核为:K(xi,xj)=(γxiTxj+coef0)degree, γ>0
- 径向基函数 RBF:K(xi,xj)=e−γ∣∣xi−xj∣∣2, γ>0
- Sigmoid 函数:K(xi,xj)=tanh(γxiTxj+coef0)
- 指数 CHI2 核:K(xi,xj)=e−γχ2(xi,xj), χ2(xi,xj)=(xi−xj)2/(xi+xj), γ>0
- 直方图相交核:K(xi,xj)=min(xi,xj)
上述的超参:
- γ:通过
SVM::setGamma(double val) 和 SVM::getGamma() 访问。
- coef0:通过
SVM::setCoef0(double val) 和 SVM::getCoef0() 访问。
- degree:通过
SVM::setDegree(int val) 和 SVM::getDegree() 访问。
关于迭代设置函数:setTermCriteria(const cv::TermCriteria &val):
- 该类变量需要3个参数:类型、迭代的最大次数、特定的阈值。
- 类型:迭代的最大次数
TermCriteria::MAX_ITER 、特定的阈值(期望精度) TermCriteria::EPS 或 MAX_ITER + EPS。
还有关于 SVM::trainAuto(...),函数如下:
1
2
3
4
5
6
7
8
| bool trainAuto( const Ptr<TrainData>& data, int kFold = 10,
ParamGrid Cgrid = getDefaultGrid(C),
ParamGrid gammaGrid = getDefaultGrid(GAMMA),
ParamGrid pGrid = getDefaultGrid(P),
ParamGrid nuGrid = getDefaultGrid(NU),
ParamGrid coeffGrid = getDefaultGrid(COEF),
ParamGrid degreeGrid = getDefaultGrid(DEGREE),
bool balanced=false) = 0;
|
- 该方法通过选择最佳参数 C、γ、p、ν、coef0、degree 来自动训练 SVM 模型。当测试集误差的交叉验证估计值最小时,参数被认为是最佳的。
- 如果不需要优化参数,则应将相应的网格步长设置为小于或等于1的任何值。
data:训练集;kFold:交叉验证参数。训练集被划分为kFold子集。一个子集用于测试模型,其他子集形成训练集;Cgrid:参数 C 的网格;gammaGrid:参数 γ 的网格;pGrid:参数 ε 的网格;nuGrid:参数 ν 的网格;coeffGrid:参数 coef0 的网格;degreeGrid:参数 degree 的网格;balanced:如果为真且问题是 2 分类,则该方法创建更平衡的交叉验证子集,即子集中的类之间的比例接近整个训练数据集中的比例。
类似地,该函数重载还有:
1
2
3
4
5
6
7
8
9
10
11
| bool trainAuto(InputArray samples,
int layout,
InputArray responses,
int kFold = 10,
Ptr<ParamGrid> Cgrid = SVM::getDefaultGridPtr(SVM::C),
Ptr<ParamGrid> gammaGrid = SVM::getDefaultGridPtr(SVM::GAMMA),
Ptr<ParamGrid> pGrid = SVM::getDefaultGridPtr(SVM::P),
Ptr<ParamGrid> nuGrid = SVM::getDefaultGridPtr(SVM::NU),
Ptr<ParamGrid> coeffGrid = SVM::getDefaultGridPtr(SVM::COEF),
Ptr<ParamGrid> degreeGrid = SVM::getDefaultGridPtr(SVM::DEGREE),
bool balanced=false) = 0;
|
例子-香蕉数据集
数据集地址:https://sci2s.ugr.es/keel/dataset.php?cod=182
该数据集十分简单,只有两个属性和一个标签。
- 属性
At1 和 At2:分别对应于x轴和y轴的两个属性。
- 标签
-1 和 +1:表示数据集中的两种香蕉形状之一。
部分数据如下表:
| At1 |
At2 |
Class |
| 0.174 |
1.92 |
-1.0 |
| 1.64 |
0.0477 |
-1.0 |
| -0.478 |
-0.796 |
-1.0 |
| -0.447 |
-1.0 |
-1.0 |
| -1.04 |
-0.2 |
1.0 |
| 2.06 |
-0.482 |
-1.0 |
使用 OpenCV 提供的 SVM 模型效果如下:
1
2
3
4
5
| Train Data imported: 5100
Test Data imported: 200
SVM算法(基于OpenCV实现):
计算花费时长:131ms
正确率:0.915
|
代码地址:Gitee - SVM
决策树
基本流程
决策树是一种非参数的监督学习方法,可用于分类和回归。
- 构造一种模型,从样本数据的特征属性中,通过决策规则,从而预测目标变量的值。
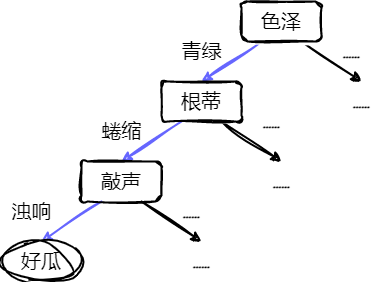
一颗决策树包含一个根结点、若干个内部结点和若干个叶结点。
- 叶结点:对应于决策结果。
- 其他每个结点对应一个属性测试。
- 根结点的范围为样本全集。
- 从根节点到每个叶结点的路径对应了一个判定测试序列。
决策树往往是自上而下,每迭代循环一次,就会选择一个特征进行分叉,直至不能再分。
- 使用“非纯度”的概念,尽量选择最佳的属性进行分叉。
- 如果一个数据集只有一种分类结果,则该集合很“纯”。
常用有熵、基尼指数和分类误差等指标定量度量:
熵Entropy=E(D)=−j=1∑Jpjlog2(pj)
基尼指数Gini=Gini(D)=j=1∑Jpj(1−pj)=1−j=1∑Jpj2=1−N2∑j=1JNj2
分类误差Error=1−max(pj)
- 上三式都是值越大,表示越不纯。
- D 表示样本数据的分类集合。
- 设集合有 J 种分类,pj 表示第 j 种分类的样本率:pj=NNj
- N 表示集合 D 中样本数据总数,Nj 表示第 j 种分类的样本数。
常用的决策树算法包括第三代迭代二叉树(ID3)、C4.5、分类和回归树(CART)。
- 前两种算法是基于熵的方法。
- CART:是基于基尼指数的方法。
ID3
易知小型决策树优于大型决策树,希望分类以后降低熵的大小。使用信息增益衡量分类后熵变小的判断:
G(D,A)=E(D)−i=1∑nNNiE(Di)
- n 表示对特征 A,样本集合被划分为 n 个不同的部分。(即 A 中包含 n 个不同的值)
- Ni 表示第 i 个部分的样本数量
- E(Di) 表示特征 A 下第 i 个部分的分类集合的熵。
信息增益越大,分类后熵的值下降得越快,分类效果越好。
C4.5
使用信息增益率进行衡量非纯度:
GR(D,A)=SI(D,A)G(D,A)
其中:
SI(D,A)=−i=1∑nNNilog2NNi
选择信息增益率最大的特征属性作为分类属性。
CART
分类树
针对特征属性 A,分类后的基尼指数为:
Ginisp(D,A)=i=1∑nNNiGini(Di)
选择分类基尼指数最小的特征属性作为分类属性。
当特征属性 A 的取值大于2时(此处讨论二叉树),需要一个阈值 β,把 D 分成 D1 和 D2。设 D1 的样本数为 L,D2 的样本数为 R,
L+R=N。
Ginisp(D,A(β))=NLGini(D1)+NRGini(D2)
Ginisp(D,A(β))=NL(1−L2∑j=1JLj2)+NR(1−R2∑j=1JRj2)=N1(L−L∑j=1JLj2+R−R∑j=1JRj2)=1−N1(L∑j=1JLj2+R∑j=1JRj2)
- ∑Lj=L,∑Rj=R
求 Ginisp 最小值变成求下式的最大值:
SG(D,A(β))L∑j=1JLj2+R∑j=1JRj2
特征为类的分类树:
采集 20 个样本来构建是否踢球分类树,设出去踢球的响应值为 1,不踢球的响应值为 0,针对风力这个特征属性,响应值为 1 的样本有 14 个,无风有 6 个样本,小风有 5 个,中风 2 个,大风 1 个,则排序的结果为:大风<中风<小风<无风。然后依据这个顺序依次按照二叉树的分叉方式把样本分为左分支和右分支,并代入式求使该式为最大值的那个分叉方式,即先把是大风的样本放入左分支,其余的放入右分支,代入式,得到 A,再把大风和中风放入左分支,其余的放入右分支,代入式,得到 B,然后把大风、中风和小风放入左分支,无风的放入右分支,计算得到 C。比较 A、B、C,如果最大值为 C,则按照 C 的分叉方式划分左右分支,其中阈值 β 可以设为 3。
特征为数值的分类树:
如一共有 14 个样本,按照由小至大的顺序为abcdefghijklmn,第一次分叉为a|bcdefghijklmn,竖线“|”的左侧被划分到左分支,右侧被划分到右分支,代入式计算其值,然后第二次分叉为 ab|cdefghijklmn,同理代入式计算其值。依次类推,得到这 13 次分叉的最大值,该种分叉方式为最佳的分叉方式,其中阈值 β 为分叉的次数。
回归树
用均方误差代替熵计算:
LS(D)=N1i=1∑N(yi−ri)2
- N 表示 D 样本数量。
- yi 表示第 i 个样本的输出值。
- ri 表示第 i 个样本的预测值。
用样本输出值的平均值代替样本的预测值:
LS(D)=N1i=1∑N(yi−N∑i=1Nyi)2=N1i=1∑N[yi2−N2yi∑i=1Nyi+N2(∑i=1Nyi)2]2=N1[i=1∑Nyi2−N2(∑i=1Nyi)2+N2(∑i=1Nyi)2]=N1[i=1∑Nyi2−N(∑i=1Nyi)2]
上式是集合 D 的最小均方误差。如果针对某特征 A,则把集合 D 划分为 s 个部分,划分后的均方误差:
LS(D,A)=i=1∑sNNiLS(Di)
- Ni 表示被划分的第 i 个集合 Di 的样本数量。
集合 D 的最小均方误差和划分后的均方误差的差值是划分为 s 个部分后的误差减小量:
ΔLS(D,A)=LS(D)−i=1∑sNNiLS(Di)
此时需要寻求最大化的误差减小量,就得到最佳的 s 个部分划分。
考虑二叉树,s=2。把 D 分成 D1 和 D2。设 D1 的样本数为 L,D2 的样本数为 R,L+R=N。
ΔLS(D,A(β))=LS(D)−NLLS(D1)−NRLS(D2)
ΔLS(D,A(β))=N1[i=1∑Nyi2−N(∑i=1Nyi)2]−NL{L1[i=1∑Lli2−L(∑i=1Lli)2]}−NR{R1[i=1∑Rri2−R(∑i=1Rri)2]}=N1[i=1∑Nyi2−N(∑i=1Nyi)2−i=1∑Lli2+L(∑i=1Lli)2−i=1∑Rri2+R(∑i=1Rri)2]=−N2(∑i=1Nyi)2+N1[L(∑i=1Lli)2+R(∑i=1Rri)2]
- yi 为集合 D 的样本响应值。
- li 为集合 D1 的样本响应值。
- ri 为集合 D2 的样本响应值。
上式除开定值,求上式最大值问题变成求下式最大值问题:
ΔLLS(D,A(β))=L(∑i=1Lli)2+R(∑i=1Rri)2
特征为类的回归树:
决策树缺失
分类树缺失响应值
如果想检测罕见的异常现象,而训练中包含的是大量正常现象,那么很可能分类结果就认为每种情况都是正常的。
可以通过设置先验概率,将异常情况的发生概率人为增加。
设 Qj 为设置的第 j 个分类的先验概率,Nj 为该分类的样本数,考虑样本率并进行归一化处理的先验概率 qj 为:
qj=∑j=1J(Qj/Nj)Qj/Nj
代入分类树的式子,得到:
SG(D,A(β),q)=∑j=1J(qjLj)∑j=1J(qjLj)2+∑j=1J(qjRj)∑j=1J(qjRj)
缺失特征属性
如果某些样本缺失了某个最佳分叉属性,如何解决:
- 把该样本删除;
- 使用各种算法估计缺失属性值;
- 用另一个特征属性代替最佳分叉属性。
CART 采用的就是计算替代分叉属性,防止最佳分叉属性缺失。
决策树剪枝
剪枝:去掉一些结点,包括叶结点和中间结点,简化树。
- 预剪枝:构建树过程中,提前终止决策树的生长;
- 后剪枝:构建树后去掉一些结点。
- 悲观错误剪枝(PEP)
- 最小错误剪枝(MEP)
- 代价复杂度剪枝(CCP)
- 基于错误剪枝(EBP)
CCP 算法会产生一系列树的序列 {T0,T1,⋯,Tm},T0 是由训练得到的最初的完整决策树,Tm 只含有一个根节点,序列中的树是嵌套的,即 Ti+1 由 Ti 剪枝得到的。
- 用 Ti+1 中的一个叶结点替代 Ti 中以该节点为根的子树。
替代的原则就是使误差的增加率 α 最小:
α=∣nt∣−1R(n)−R(nt)
- R(n) 表示 Ti 中结点 n 的预测误差;
- R(nt) 表示 Ti 中以结点 n 为根结点的子树的所有叶结点的预测误差之和;
- ∣nt∣ 表示该子树叶结点的数量,nt 也被称为复杂度。
- α 的含义是用一个结点 n 来替代以 n 为根节点的所有 ∣nt∣ 个结点的误差增加的规范化程度。
在 Ti 中,选择最小的 α 值的结点进行替代,得到 Ti+1。每需要得到一棵决策树,都需要计算其前一棵决策树的 α 值,根据 α 值进行剪枝,最终直至 Tm。
分类树的情况,如果使用分类误差来表示结点 n 的预测误差,则:
R(n)=∑j=1mNj∑j=1mNj−max{Nj}=NN−max{Nj}
- Nj 表示结点 n 下第 j 个分类的样本数;
- N 表示该结点的所有样本数;
- max{Nj} 表示在 m 个分类中,拥有样本数最多的那个分类的样本数量。
回归树的情况,可以使用集合 D 的最小均方误差表示结点 n 的预测误差:
R(n)=N∑i=1N(yi2)−N(∑i=1Nyi)2
- yi 表示第 i 个样本的响应值;
- N 为该结点的样本数量。
用全部样本得到的决策树序列为 {T0,T1,⋯,Tm},其对应值 α0<α1<⋯<αm。下一步是从这个序列最优选择一颗决策树 Ti,常用交叉验证法。
OpenCV提供的DTree
DTrees 类表示一个决策树或一组决策树。类的当前公共接口允许用户只训练单个决策树,但是类能够存储多个决策树并使用它们进行预测(通过求和响应或使用投票方案),以及从DTree类派生的类(如RTree和Boost)使用此功能来实现决策树集成。
该类中有部分参数解释:
MaxCategories:表示特征属性为类的形式的最大类数量。如果训练过程中,类的数量大于该值,采用聚类方法更高效。该参数只应用于非两类的分类树问题。通过以下函数访问:
1
2
| int getMaxCategories();
void setMaxCategories(int val);
|
MaxDepth:决策树的最大可能深度。通过以下函数访问:
1
2
| int getMaxDepth();
void setMaxDepth(int val);
|
MinSampleCount:如果某个结点的样本数小于该值,则该结点不再被分叉。通过以下函数访问:
1
2
| int getMinSampleCount();
void setMinSampleCount(int val);
|
CVFolds:表示交叉验证的子集数量。如果值大于1,则应该交叉验证进行剪枝。通过以下函数访问:
1
2
| int getCVFolds();
void setCVFolds(int val);
|
UseSurrogates:如果设为真,则需要产生代替分叉节点。默认为假。通过以下函数访问:
1
2
| bool getUseSurrogates();
void setUseSurrogates(bool val);
|
Use1SERule:如果设为真,表示剪枝过程使用 1SE 规则,使决策树更加的,且对训练集的噪声更有抵抗力,但精度会下降。默认为真。通过以下函数访问:
1
2
| bool getUse1SERule();
void setUse1SERule(bool val);
|
TruncatePrunedTree:如果设为真,则要被剪掉的结点将从树上移除,否则仍保留。默认为真。通过以下函数访问:
1
2
| bool getTruncatePrunedTree();
void setTruncatePrunedTree(bool val);
|
RegressionAccuracy:构建回归树的条件,表示回归树的响应值的精度如果达到该值则无需再分叉。通过以下函数访问:
1
2
| float getRegressionAccuracy();
void setRegressionAccuracy(float val);
|
Priors:表示分类树的类别标签先验概率,按类别标签值排序。通过以下函数访问:
1
| cv::Mat getPriors()void setPriors(const cv::Mat &val);
|
例子-单词难度预测
数据集地址:https://aistudio.baidu.com/datasetdetail/107161
数据集属性有:
- Word:单词
- Length:长度
- Freq_HAL:频率_HAL
- Log_Freq_HAL:对数频率HAL
- I_Mean_RT
- I_Zscore:确定单词的难度。对于一个单词,此值在0和1之间波动,其中0为简单,1为困难
- I_SD
- Obs
- I_Mean_Accuracy:准确性,为响应值
部分数据如下:
| Length |
Freq_HAL |
Log_Freq_HAL |
I_Mean_RT |
I_Zscore |
I_SD |
Obs |
I_Mean_Accuracy |
| 1.00 |
10610626.00 |
16.18 |
798.92 |
-0.01 |
333.85 |
24.00 |
0.73 |
| 3.00 |
222.00 |
5.40 |
816.43 |
0.21 |
186.03 |
21.00 |
0.62 |
| 5.00 |
10806.00 |
9.29 |
736.06 |
-0.11 |
289.01 |
32.00 |
0.97 |
| 5.00 |
387.00 |
5.96 |
796.27 |
0.11 |
171.61 |
15.00 |
0.45 |
| 6.00 |
513.00 |
6.24 |
964.40 |
0.65 |
489.00 |
15.00 |
0.47 |
效果如下:
1
2
3
4
5
| Train Data imported: 30457
Test Data imported: 9992
决策树算法(基于OpenCV实现):
计算花费时长:159ms
平均误差:0.0239817
|
代码地址:Gitee - Decision Tree
AdaBoost
基本流程
自适应提升(Adaptive Boosting,AdaBoost)算法,可作为一种从一系列弱分类器中产生一个强分类器的通用方法。
假设有一个集合 {(x1,y1),(x2,y2),…,(xN,yN)},xi 表示特征矢量;yi 表示对应分类为 {−1,1} 的标签。
AdaBoost 算法通过 M 次迭代得到若干个弱分类器 {k1,k2,…,kM},对于每个样本,弱分类器都会给出分类结果 km(xi)∈{−1,1}。
将 M 个弱分类器进行某种线性组合,得到一个强分类器 Cm。
进行第 m−1 次迭代后,线性组合得到的强分类器为:
Cm−1(xi)=α1k1(xi)+α2k2(xi)+⋯+αm−1km−1(xi)(1)
- αi 为权值,m>1。
进行第 m 次迭代时,AdaBoost通过增加一个弱分类器的方式扩展成一个强分类器:
Cmxi=Cm−1(xi)+αmkm(xi)(2)
定义误差 E,判断 Cm 和 Cm−1 的性能,当 Cm 比 Cm−1 的效果强才有意义。误差用所有样本 xi 的指数损失的总和定义:
E=i=1∑Ne−yiCm(xi)=i=1∑Ne−yi(Cm−1(xi)+αmkm(xi))(3)
令 wi(m) 表示在第 m−1 次迭代后,对训练样本 xi 所分配的权重。
- wi(1)=1,wi(m)=e−yiCm−1(xi)
E=i=1∑Nwi(m)e−yiαmkm(xi)(4)
将上式拆成:
E=yi=km(xi)∑wi(m)e−αm+yi=km(xi)∑wi(m)eαm(5)
- 若 yi=km(xi),则分类结果与实际相符,无论都为 −1 还是 1,乘积为 1。
- 若 yi=km(xi),则分类结果与实际不符,乘积为 −1。
根据对所有 yi=km(xi) 的数据项 xi 的误差求和,对所有 yi=km(xi) 的数据项 xi 的误差求和,再改写成:
E=yi=km(xi)∑wi(m)e−αm+yi=km(xi)∑wi(m)eαm=i=1∑Nwi(m)e−αm+yi=km(xi)∑wi(m)(eαm−e−αm)(6)
可以看出,如果 αm 一定,强分类器 Cm 的误差大小完全取决于第二项中 ∑yi=km(xi)wi(m) 的大小,即取决于这次迭代中被错分类的权值 wi(m) 的大小。
对式5进行求导:
dαmdE=yi=km(xi)∑wi(m)eαm−yi=km(xi)∑wi(m)e−αm(7)
令导数为0,得到权值 αm:
αm=21ln(∑yi=km(xi)wi(m)∑yi=km(xi)wi(m))(8)
令 ϵm 表示误差率:
ϵm=∑i=1Nwi(m)∑yi=km(xi)wi(m)(9)
则 αm 写成:
αm=21ln(ϵm1−ϵ)(10)
得到 AdaBoost 算法:每次迭代中,选择使 ∑yi=km(xi)wi(m) 最小的分类器 km,得到误差率 ϵm,从而计算权值 αm,则最终强分类器由 Cm−1 逐渐提升为 Cm=Cm−1+αmkm。
每次迭代后,得到每个训练样本数据权值 wi(m+1) 为:
wi(m+1)=wi(m)e−yiαmkm(xi)=wi(m)×{e−αm,eαm,分类正确分类错误(11)
AdaBoost的计算步骤:
- 设有 n 个样本 x1,…,xn,分类为 y1,…,yn,yi∈{−1,1}。
- 初始化每个样本的权值 w1(1),…,wn(1),都为 n1。
- 进行迭代:m=1,…,M。
- 找到使得错误率 ϵm 最小的弱分类器 km(x),并得到 ϵm(见式9)。
- 计算 km(x) 的权值 αm(见式10)。
- 得到新的强分类器 Cm(x)(见式2)。
- 更新每个样本的权值 wi(m+1)(见式11)。
- 对权值 wi(m+1) 进行归一化,使 ∑iwi(m+1)=1。
- 得到最终的强分类器:
C(x)=sign(CM(x))=sign(i=1∑Mαmkm(x))(12)
AdaBoost 算法可分为 Discrete AdaBoost、Real AdaBoost、LogitBoost 和 Gentle AdaBoost。
- Discrete AdaBoost 的弱分类输出结果是 1 或 -1,组成强分类器时是离散的形式。
- Real AdaBoost的弱分类器输出结果是该样本属于某一类的概率。
上述讨论即为 Discrete AdaBoost 的迭代过程。
Real AdaBoost 的迭代过程:
- 基于每个样本的权值 wi(m),拟合一个分类概率估计 pm(x)=P(y=1∣x)∈[0,1],表示样本属于分类结果为1的概率。
- 得到这次迭代的弱分类器:km(x)=21ln(1−pm(x)pm(x))。
- 更新权值:wi(m+1)=wi(m)e−yikm(x)。
- 归一化权值。
最终强分类器 C 为:
C(x)=sign(i=1∑Mkm(x))(13)
LogitBoost 是逻辑回归技术在 AdaBoost 的应用。弱分类器的选取基于加权最小二乘法。
设迭代前强分类器 C0(x)=0,每个训练样本数据的概率估计 p0(xi)=0.5,迭代过程如下:
- 计算工作响应 zi(m):
zi(m)=pm−1(xi)[1−pm−1(xi)]yi∗−pm−1(xi)(14)
yi∗=2yi−1(15)
- 计算权值:
wi(m)=pm−1(xi)[1−pm−1(xi)](16)
-
应用权值 wi(m),基于 zi(m) 到 xi 的加权最小二乘回归法,拟合弱分类器 km(xi)。
-
更新 pm(xi)
pm(xi)=eCm−1(xi)+e−Cm−1(xi)eCm−1(xi)=1+e−2Cm−1(xi)1(17)
- 更新强分类器。
Cm(xi)=Cm−1(xi)+21km(xi)(18)
最终强分类器为式13。
Gentle AdaBoost 算法与 LogitBoost 算法相似,但参数选择更简单。弱分类器 km(x) 由基于权值 wi(m) 的从 yi 到 xi 的加权最小二乘法回归拟合得到。
每次迭代得到的强分类器 Cm(x) 和 权值:
Cm(xi)=Cm−1(xi)+km(xi)(19)
wi(m+1)=wi(m)e−yikm(xi)(20)
OpenCV提供的AdaBoost
OpenCV 实现了上述4种 AdaBoost,且弱分类器都采用 CART 决策树的方法。
使用决策树时:
αm=ln(ϵm1−ϵ)(21)
wi(m+1)=wi(m)×{1,eαm,分类正确分类错误(22)
OpenCV 的 ml 中提供了Boost 类,继承自 DTree 类。
类中有部分参数:
BoostType:Boosting 算法的类型。
1
2
3
4
5
6
7
8
9
10
| enum Types
{
DISCRETE=0,
REAL=1,
LOGIT=2,
GENTLE=3
};
int getBoostType();
void setBoostType(int val);
|
WeakCount:弱分类器的数量,也是迭代次数。访问函数:
1
2
| int getWeakCount();
void setWeakCount(int val);
|
WeightTrimRate:裁剪率,0~1,在迭代过程中,那些归一化后的样本权值 wi(m) 小于该裁剪率的样本将不进入下次迭代。访问函数:
1
2
| double getWeightTrimRate();
void setWeightTrimRate(double val);
|
例子-用户贷款违约预测
数据集地址:https://aistudio.baidu.com/datasetdetail/112664
数据集的属性如下:
- income:用户收入,较大数
- age:用户年龄
- experience_years:用户从业年限
- is_1:是否单身
- city:居住城市,抽象代号
- region:居住地区,抽象代号
- current_job_years:现任职位工作年数
- current_house_years:现居房屋居住年数
- house_ownership:房屋所有权,租用(1)、自有(2)、未有(0)
- car_ownership:是否拥有汽车
- profession:职业,抽象代号
- label:是否存在违约,即响应值
AdaBoost 分类效果如下:
1
2
3
4
5
| Train Data imported: 168000
Test Data imported: 84000
AdaBoost算法(基于OpenCV实现):
计算花费时长:31247ms
准确率:0.890024
|
代码地址:Gitee - AdaBoost
随机森林
森林由若干棵树组成。
随机森林由若干棵决策树组成,每棵决策树之间互不相关。
随机体现在:
- 通过 随机 抽取得到不同的样本,来构建每棵决策树。
- 决策树每个节点的最佳分叉属性从由 随机 得到的特征属性集合中选取。
预测时,预测样本作用于所有决策树。
- 对于分类问题,利用投票方式得到分类。
- 对于回归问题,取所有决策树结果的平均值。
随机过程
Bootstrap 过程
Bootstrap过程:生成每棵决策树时,使用的参数相同,但使用的训练集不同。
在 Bootstrap 集合的基础上聚集得到学习模型的过程称为 Bagging(Bootstrap aggregating)。
不在 Bootstrap 集合中的样本称为 OOB(Out Of Bag)。
Bootstrap 过程:从全部 N 个样本中,有放回的随机抽取 S 次(OpenCV中,S=N),其中存在 OOB。计算 OOB 样本所占比率:
- 每个样本被抽取的概率为 1/N,未被抽取的概率为 1−1/N,S 次仍未被抽到的概率为 (1−1/n)S,limN=S→∞(1−N1)S=e−1。
随机森林中每棵决策树的 bootstrap 集合是不完全相同的,每棵决策树的 OOB 集合也不完全相同。
即每棵生成决策树之前,进行 Bootstrap 过程。
- 保证 bootstrap 集合不同,保证了每棵决策树不相关以及不相同。
随机特征属性过程
随机森林的决策树的最佳分叉属性是在一个特征属性随机子集内计算得到。
- 全部的 p 个特征属性中,随机选择 q 个特征属性。
- 对于分类问题,q 可以为 p 的平方根。
- 对于回归问题,q 可以为 p 的三分之一。
随机子集内特征属性的数量 q 是固定的,但不同决策树之间这 q 个特征属性不同。
- 由于 q 远小于 p,构建决策树时无需剪枝。
OOB误差
评估机器学习算法的预测误差的常用方法时交叉验证法,但 Bagging 方法不需要交叉验证。
OOB 误差可以代替 bootstrap 集合误差,结果近似于交叉验证。
- OOB 误差是利用那 e−1 的 OOB 样本来评估预测误差。
OOB 误差计算是在训练过程同步得到。每得到一棵决策树,就可以根据该决策树来调整前面决策树得到的 OOB 误差。
对于分类问题, OOB 误差计算:
- 构建生成决策树 Tk,k=1,2,...,K。
- 用 Tk 预测 Tk 的 OOB 样本的分类结果。
- 更新所有训练样本的 OOB 预测分类结果次数(如果样本 x 是 T1 的 OOB 样本,则它有一个预测结果,而它是 T2 的 bootstrap 集合内的样本,则此时它没有预测结果)。
- 对所有样本,把每个样本的预测次数最多的分类作为该样本在 Tk 时的预测结果。
- 统计所有训练样本中预测错误的数量。
- 该数量除以 Tk 的 OOB 样本的数量作为 Tk 的 OOB 误差。
对于回归问题, OOB 误差计算:
- 构建生成决策树 Tk,k=1,2,...,K。
- 用 Tk 预测 Tk 的 OOB 样本的回归值。
- 累加所有训练样本中的 OOB 样本的预测值。
- 对所有样本,计算 Tk 时每个样本的平均预测值(预测累加值除以被预测的次数)。
- 累加每个训练样本平均预测值与真实响应值之差的平方。
- 该平方累加和除以 Tk 的 OOB 样本的数量作为 Tk 的 OOB 误差。
OOB 误差会逐渐缩小,设置精度 ε,当误差小于 ε 时,提前终止迭代。
计算特征属性的重要性
特征属性的重要性:样本哪个特征属性对预测起决定作用。
Gini 法和置换法常用于计算特征属性的重要性。
Gini 法依据不纯度减小的原则。
置换法依据原则为:样本某个特征属性越重要,那么改变该特征属性值,则样本预测值就越容易出错。
- 通过置换两个样本的相同特征属性的值来改变特征属性。
具体方法:
在决策树 Tk 的 OOB 集合中随机选择两个样本 xi=(xi,1,xi,2,…,xi,p) 和 xj=(xj,1,xj,2,…,xj,p),这两个样本响应值分别为 yi 和 yj,用 Tk 的预测值分别为 y^i(k) 和 y^j(k)。
设该 OOB 集合有 mk 个样本。衡量第 q 个特征属性的重要性,置换 xi 和 xj 中的 xi,q 和 xj,q,置换后为:xi,jq=(xi,1,…,xj,q,…,xi,p) 和 xj,iq=(xj,1,…,xi,q,…,xj,p)
根据这个方法,对 OOB 集合共置换 mk 次,最终置换结果为:xi,mq=(xi,1,…,xmi,q,…,xi,p)。
使用 Tk 对 xi,mq 的预测值为 y^i,mq(k)。
对于分类问题:
- 如果 y^i,mq(k)=yi,说明改变第 q 个特征属性的值,并不改变最终的响应值。
- 如果 y^i,mq(k)=yi,说明第 q 个特征属性很重要。
重要程度量化为:
VIq(k)=mk∑i∈mkI(yi=y^i(k))−∑i∈mkI(yi=y^i,mq(k))
- 分子第一项表示对 OOB 中,预测正确的样本数量。
- 分子第二项表示置换后正确的样本数量。
对于回归问题,重要程度量化为:
VIq(k)=mk∑i∈mke−(Ayi−y^i(k))2−∑i∈mke−(Ayi−y^i,mq(k))2
其中,
A=i∈Nmax∣yi∣
如果第 q 个特征属性不属于 Tk,则 VIq(k)=0。
对随机森林的所有决策树都计算第 q 个特征属性的重要性,取平均得到整个随机森林对第 q 个特征属性的重要程度量化为:
VIq=K∑i=1KVIq(i)
归一化处理:
VIq(1)=∑i=1pVIiVIq
OpenCV 提供的随机森林
OpenCV 提供了一个 继承自 DTree 的 RTree 类,可用于设计随机森林。
部分参数如下:
CalculateVarImportance:表示是否计算特征属性的重要程度。函数接口:
1
2
3
4
| bool getCalculateVarImportance();
void setCalculateVarImportance(bool val);
|
ActiveVarCount:在每棵树结点处随机选择的特征子集的大小,以及所使用的找到最佳分割点。如果将其设置为0,则大小将设置为特征总数的平方根。函数接口:
1
2
| int getActiveVarCount() ;
void setActiveVarCount(int val);
|
还有些参数通过 DTree 的函数设置。
例子-单词难度预测(RTrees)
该数据集在决策树中也使用过,故不多介绍。
数据集属性有:
- Word:单词
- Length:长度
- Freq_HAL:频率_HAL
- Log_Freq_HAL:对数频率HAL
- I_Mean_RT
- I_Zscore:确定单词的难度。对于一个单词,此值在0和1之间波动,其中0为简单,1为困难
- I_SD
- Obs
- I_Mean_Accuracy:准确性,为响应值
使用决策树和随机森林的效果如下:
1
2
3
4
5
6
7
8
9
10
11
| Train Data imported: 30457
Test Data imported: 9992
决策树算法(基于OpenCV实现):
计算花费时长:186ms
平均误差:0.0239817
Train Data imported: 30457
Test Data imported: 9992
随机森林算法(基于OpenCV实现):
计算花费时长:17378ms
平均误差:0.0212776
|
代码地址:Gitee - Random Trees
神经网络
神经网络是一种模仿生物神经系统的机器学习算法。
神经元
人工神经网络由若干个神经元构成。神经元结构如下:

- x1、x2、...、xn 是神经元的输入。
- y 是神经元的输出。
- w1、w2、...、wn 是神经元的权重。
- b 为偏移量。
神经元内部包括两个部分:
- 输入的加权求和;
u=i=1∑n(wixi)+b=i=0∑n(wixi),x0恒为1
- 对求和结果的“激活”。激活指的是对输出值进行某种关系映射,使得神经元兴奋或抑制。
y=f(u)
激活函数有多种:
线性函数:
f(x)=x
阈值函数:
f(x)={1,0,x≥θx<θ
Sigmoid 函数:
f(x)=1+e−x1
对称 Sigmoid 函数:
f(x)=β1+e−αx1−e−αx
双曲正切函数:
f(x)=ex+e−xex−e−x
高斯函数:
f(x)=βe−α2x2
RELU 函数:
f(x)=max(0,x)
感知器
感知器由两层神经元组成:
感知器的学习规则很简单,对于训练样本 (x,y),若当前感知机输出为 y^,则权重调整为:
wi=wi+Δwi=wiη(y−y^)xi
- η∈(0,1) 称为学习率。
感知器只有输出层神经元进行激活函数处理,也就是只有一层功能神经元,处理线性可分问题。
- 存在一个线性超平面将样本分开,则感知器的学习过程会收敛。
多层感知器 MLP
解决非线性可分问题,需要考虑多层(功能)神经元。
前馈神经网络是神经网络的一种,包括一个输入层、一个输出层和若干个隐含层。
- 某一层的神经元只能通过一个方向连接到下一层的神经元。
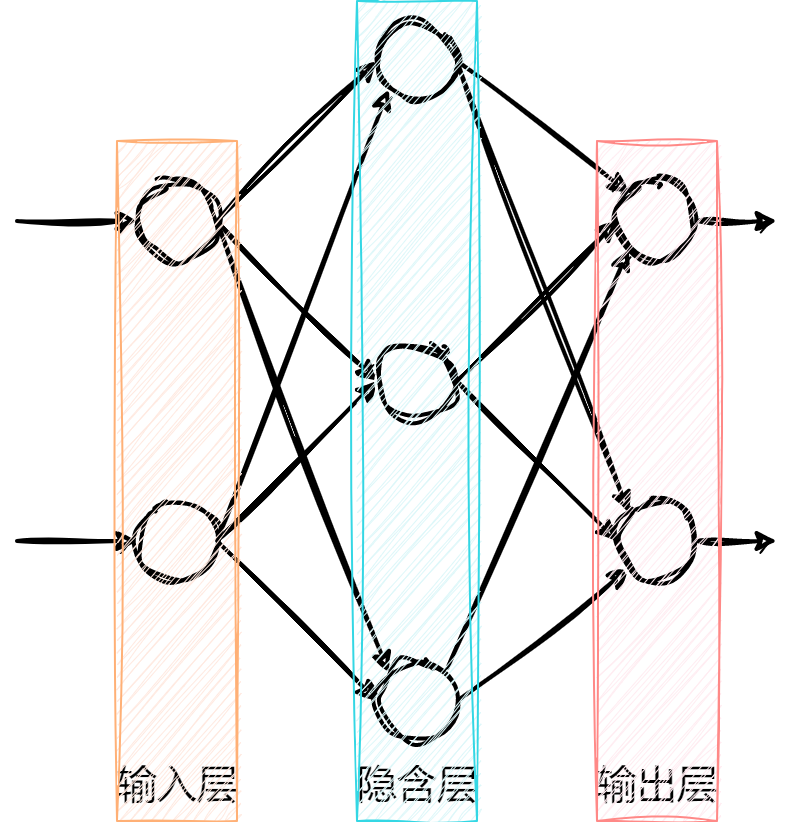
像上图这种拓扑结构的神经网络又称为多层感知器(MLP,Multi-Layer Perceptron)。
MLP 可以用 Backprop(backward propagation of errors,误差反向传播,BP)算法实现建模。
BP 算法输入层的神经元数量一般为样本的特征属性数量,输出层的神经元的数量一般为样本的所有可能目标值的数量。
BP 算法的核心思想是:通过前向通路得到误差,再把误差反向传播,实现权值的修正。
MPL 的误差可以用平方误差函数表示。
- 设某个样本 x=(x1,x2,...,xn) 对应的目标值为 t,有 J 种可能值,t={t1,t2,...,tj}。
- 则 MLP 输入层一共有 n 个神经元,输出层(第 L 层)有 J 个神经元。
设样本 x 经过前向通路得到的最终输出为 y={y1L,y2L,...,yjL}。
则该样本的平方误差为:
E=21j=1∑J(tj−yjL)2
- 21 为方便求导系数,不影响误差的变化趋势。
MLP 的目标是使得 E 最小。通过改变权值 w,从而使得 E 最小。
Backprop算法是一种迭代的方法,渐进地减小 E。
误差 E 对权值 w 的导数为 w 的变化率:
Δw=−ηdwdE
- η∈(0,1) 表示学习效率,控制收敛速度和准确性。
- η 过大,导致震荡,很难收敛;
- η 过小,导致长时间不能收敛。
引入“动量” μ,改变因 η 的选取不好而带来的问题,上式改写为:
Δw(t)=−ηdwdE(t)+μΔw(t−1)
- t 表示当前,t−1 表示上一次,t+1 表示下一次。
- 说明本次的 w 变化率不仅与 E 的导数相关,还与上一次 w 的变化率相关。
- μ 提供了一些惯性,使之平滑权值的随机波动。
由 Δw 更新当前权值 w:
w(t+1)=w(t)+Δw(t)
- 上式表示了更新权值的过程是从输出层到隐含层,向输入层逐层推进的过程,即误差的反向传播。
当所有权值更新完后,再由前向通路计算得到新的误差 E,完成一次迭代。
具体计算过程
设 wkhl 表示第 l 层的第 k 个神经元与第 l−1 层的第 h 和神经元之间连接的权值。第 l 层的第 k 个神经元的输出 ykl 为:
ykl=f(ukl)=f(h=1∑H(wkhlyhl−1)+bkl)
- ukl 表示第 l 层第 k 个神经元的加权和;
- bkl 表示第 l 层第 k 个神经元的偏置。
若第 l 层共有 K 个神经元,第 l−1 层共有 H 个神经元,则第 l 层的 K 个神经元的加权和 ul 可以用矩阵表示:
ul=⎝⎜⎜⎜⎜⎛u1lu2l⋮uKl⎠⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎛w11lw21l⋮wK1lw12lw22l⋮wK2l⋯⋯⋱⋯w1Hlw2Hl⋮wKHl⎠⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎛y1l−1y2l−1⋮yHl−1⎠⎟⎟⎟⎟⎞+⎝⎜⎜⎜⎜⎛b1lb2l⋮bKl⎠⎟⎟⎟⎟⎞
第 l 层的所有 K 个神经元输出 yl 为:
yl=⎝⎜⎜⎜⎜⎛y1ly2l⋮yKl⎠⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎛f(u1l)f(u2l)⋮f(uKl)⎠⎟⎟⎟⎟⎞=f(ul)
把每层的输出 yl 级联在一起,就构成了 MLP 的前向通路。
- 当一个样本添加到输入层时,通过层层计算得到最终输出 yL,再代入误差计算中得到误差。
前向通路过程为,样本进行权值计算,通过激活输出,最后得到误差:
wkhl→ukl→ykl→E
计算权值变化率,即对误差求导,由链式法则可知,样本 x 的误差 E 对权值 wkhl 的偏导数为:
∂wkhl∂E=∂ykl∂E∂ukl∂ykl∂wkhl∂ukl
- 定义 δkl 为上式等号右侧的前两项偏导,δkl=∂ykl∂E∂ukl∂ykl=∂ukl∂E
计算上式等号右侧第三个偏导,有:
∂wkhl∂ukl=∂wkhl∂[h=1∑H(wkhlyhl−1)+bkl]∂wkhl∂ukl=∂wkhl∂(wk1ly1l−1+⋯+wkhlyhl−1+⋯+wkHlyHl−1+bkl)∂wkhl∂ukl=yhl−1
- 求导的结果为第 l−1 层的第 h 个神经元的输出。如果第 l−1 为输入层,则 yhl−1 为样本的第 h 个属性。
计算上式等号右侧第二个偏导,有:
∂ukl∂ykl=∂ukl∂f(ukl)=f′(ukl)
- f(⋅) 表示激活函数。
- 线性函数求导为:dxdf(x)=dxdx=1。
- Sigmoid 函数求导为:dxdf(x)=dxd(1+e−x1)=1+e−x1(1−1+e−x1)=f(x)(1−f(x))
- 对称 Sigmoid 函数求导为: dxdf(x)=dxd(β1+e−αx1−e−αx)=2αβ(1+e−αx)2e−αx
- 双曲正切函数求导为:dxdf(x)=dxd(ex+e−xex−e−x)=1−f2(x)
- 高斯函数求导为: dxdf(x)=dxd(βe−α2x2)=−2α2βxe−α2x2
计算上式等号右侧第一个偏导,当 ykl 为输出层的输出时,即 yjL,有:
∂yjL∂E=∂yjL∂[21j=1∑J(tj−yjL)2]∂yjL∂E=∂yjL∂[21(t1−y1L)2+⋯+21(tj−yjL)2+⋯+21(tJ−yJL)2]∂yjL∂E=yjL−tj
所以,基于输出层的权值 yjhL 误差导数为:
∂wjhL∂E=(yjL−tj)f′(ujL)yhL−1
- δjL=(yjL−tj)f′(ujL)
不知道内部神经元的输出误差,只知道输出层的误差,所以需要把内部神经元误差传递到输出层。
- 又因为神经元都直接或间接地相互连接,所以内部所有神经元的误差最终都会传递到输出层的所有神经元上。
设 yhl 为中间第 l 层的第 h 个神经元的输出,则:
∂yhl∂E=∂yhl∂[E(u1l+1),⋯,E(uKl+1)]
- E(ukl+1) 表示误差 E 是关于 ukl+1 的函数。
上式表明,第 l 层的第 h 个神经元的输出误差传递到第 l+1 层内的所有 K 个神经元内,则:
∂yhl∂E=k=1∑K(∂ukl+1∂E∂yhl∂ukl+1)
计算右侧第二个偏导:
∂yhl∂ukl+1=∂yhl∂[h=1∑H(wkhl+1yhl)+bkl+1]∂yhl∂ukl+1=∂yhl∂(wk1l+1y1l+⋯+wkhl+1yhl+⋯+wkHl+1yHl+bkl+1)∂yhl∂ukl+1=wkhl+1
计算右侧第一个偏导:
∂ukl+1∂E=δkl+1
所以,基于中间层的权值 wkhl 的误差导数为:
∂wkhl∂Ep=[k=1∑K(wkhl+1δkl+1)]f′(ukl)yhl−1
先得到输出层的结果,再计算倒数第二层,以此类推,完整的误差导数:
∂wkhl∂E=δklyhl−1,其中δkl={(ykl−tk)f′(ukl),[∑k=1K(wkhl+1δkl+1)]f′(ukl),l为输出层l为中间层
把上式的结果代入计算得到 权值的变化率。再由 w(t+1)=w(t)+Δw(t) 得到更新后的权值。经过新权值计算下一样本,反复进行。
计算的方法:
- 在线方法:样本一个一个地进入 MLP,每完成一个样本的计算,就更新一次权值。
- 为了增加鲁棒性,每次迭代之前,可以把全体样本打乱顺序,这样在每次迭代的过程中,提取样本的顺序就会不相同。
- 批量方法:把所有样本的误差累加在一起,用该累加误差计算误差的导数,进而得到权值的变化率。
初始化权值
一般会随机选择很小的值作为初始权值。
采用 Nguyen-Widrow 算法初始化权值:
- 每个神经元都有属于自己的一个区间范围,通过初始化权值就可以限制它的区间位置。当改变权值时,也在自己的区间范围内变化。
Nguyen-Widrow 算法初始化 MLP 权值的方法为:
- 对于所有连接输出层的权值和偏移量,初始值为在 −1 到 1 之间的随机数;
- 对于中间层的权值,初始化为(νh 为 −1 到 1 之间的随机数,H 为第 l−1 层神经元的数量):
wkhl=∑h=1H∣νh∣νh
- 对于中间层的偏移量,初始化为(νk 为 −1 到 1 之间的随机数,K 为第 l 层神经元的数量):
bkl=(K2k−1)νkG
G=0.7HK−11
RPROP
上述 BP 算法的权值变化基于误差梯度的变化率。
而 RPROP 算法的权值变化基于它的符号:
Δw(t)=⎩⎪⎪⎨⎪⎪⎧−Δ(t),+Δ(t),0,∂w∂E(t)>0∂w∂E(t)<0其他
其中,
Δ(t)=⎩⎪⎪⎨⎪⎪⎧η+Δ(t−1),η−Δ(t−1),Δ(t−1),∂w∂E(t−1)∂w∂E(t)>0∂w∂E(t−1)∂w∂E(t)<0其他
- 常数 η+ 必须大于1;
- 常数 η− 必须在0~1之间。
- ∂E/∂w 由下式得到:
∂wkhl∂E=δklyhl−1,其中δkl={(ykl−tk)f′(ukl),[∑k=1K(wkhl+1δkl+1)]f′(ukl),l为输出层l为中间层
- Δ(0)=0.1 比较好;
- Δmax(t)=50,Δmin(t)=10−6 可以防止溢出。
OpenCV 提供的 ANN
OpenCV 提供的神经网络算法有:
1
2
3
4
5
6
| enum TrainingMethods
{
BACKPROP=0,
RPROP = 1,
ANNEAL = 2
};
|
通过函数设置:
1
2
3
4
5
6
7
8
9
10
11
|
void setTrainMethod(int method, double param1 = 0, double param2 = 0);
int getTrainMethod();
|
OpenCV 提供的激活函数(目前,默认和唯一完全支持的激活函数是对称 Sigmoid):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| enum ActivationFunctions
{
IDENTITY = 0,
SIGMOID_SYM = 1,
GAUSSIAN = 2,
RELU = 3,
LEAKYRELU= 4
};
|
通过函数设置:
1
2
3
|
void setActivationFunction(int type, double param1 = 0, double param2 = 0);
|
部分参数如下:
LayerSizes:指定每层神经元的数量,包括输入和输出层。参数为向量,第一个元素指定了输入层中元素的数量。最后一个元素为输出层中元素的数量。默认值为空。
1
2
| void setLayerSizes(InputArray _layer_sizes);
cv::Mat getLayerSizes() const = 0;
|
BackpropWeightScale:权重梯度项的强度,
推荐值为0.1左右,默认值为0.1。
1
2
| double getBackpropWeightScale();
void setBackpropWeightScale(double val);
|
BackpropMomentumScale:动量项的强度,该参数提供了一些惯量来平滑权重的随机波动。默认值为0.1。
1
2
| double getBackpropMomentumScale();
void setBackpropMomentumScale(double val);
|
propDW0:RPROP 中的 Δ0,默认值为0.1。
1
2
| double getRpropDW0();
void setRpropDW0(double val);
|
RpropDWPlus:RPROP 中的增加因子 η+,默认值为1.2。
1
2
| double getRpropDWPlus();
void setRpropDWPlus(double val);
|
RpropDWMinus:RPROP 中的减少因子 η−,默认值为0.5。
1
2
| double getRpropDWMinus();
void setRpropDWMinus(double val);
|
RpropDWMin 和 RpropDWMax:RPROP 中的 Δmin(t) 和 Δmax(t)
1
2
3
4
5
6
7
|
double getRpropDWMin();
void setRpropDWMin(double val);
double getRpropDWMax();
void setRpropDWMax(double val);
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
double getAnnealInitialT();
void setAnnealInitialT(double val);
double getAnnealFinalT();
void setAnnealFinalT(double val);
double getAnnealCoolingRatio();
void setAnnealCoolingRatio(double val);
int getAnnealItePerStep();
void setAnnealItePerStep(int val);
void setAnnealEnergyRNG(const RNG& rng);
|
例子-糖尿病预测(MLP)
数据集在贝叶斯分类器学习记录中使用过,详见贝叶斯分类器。
数据集属性如下:
- Pregnancies: 怀孕次数
- Glucose:血浆葡萄糖浓度
- BloodPressure:舒张压
- SkinThickness:肱三头肌皮肤褶皱厚度
- Insulin:两小时胰岛素含量
- BMI:身体质量指数,即体重除以身高的平方
- DiabetesPedigreeFunction:糖尿病血统指数,即家族遗传指数
- Age:年龄
使用 MLP 进行预测结果与贝叶斯分类器比较如下:
1
2
3
4
5
6
7
8
9
10
11
| Train Data imported: 668
Test Data imported: 100
正态贝叶斯分类器:
计算花费时长:0ms
正确率:0.76
Train Data imported: 668
Test Data imported: 100
神经网络(BP)算法(基于OpenCV实现):
计算花费时长:230ms
正确率:0.82
|
代码地址:Gitee - ANN_MLP











